Chapter 6 Nonparametric Estimations - Basics

The models we see in the previous chapters are parametric, which means that they have to assume a certain structure on the regression function \(m\) controlled by parameters before the estimations. Therefore, the results from parametric models are the best for estimating \(m\), if and only if their model specifications are correct. Avoiding this assumption is the strongest point of nonparametric methods, which do not require any hard-to-satisfy pre-determined regression functions.

Before talking about a nonparametric estimator for the regression function \(m\), we should first look at a simple nonparametric density estimation of the predictor \(X\). This estimator is aimed to estimate \(f(x)\), the density of \(X\), from a sample and without assuming any specific form for \(f\). That is, without assuming, for example, that the data is normally distributed. Therefore, we first start with nonparametric density estimations.

6.1 Density Estimations

We are only going to look at one-variable Kernel density estimation. Let’s assume that a sample of \(n\) observations, \(y_1,...,y_n\), is drawn from a parametric distribution \(f(y,\theta)\). If the data are i.i.d., the joint density function is:

\[\begin{equation} f(y;\theta)=\prod_{i=1}^{n} f\left(y_{i} ; \theta\right) \tag{6.1} \end{equation}\]

To estimate the parameters that maximize this density function (“likelihood”), or more easily, its logarithmic transformation:

\[\begin{equation} \ell(y ; \theta)=\log f(y ; \theta)=\sum_{i=1}^{n} \log f\left(y_{i} ; \theta\right) \tag{6.2} \end{equation}\]

We use MLE to estimate \(\theta\). This is called parametric estimation and if our pre-determined density model is not right, that is, if \(f\) is misspecified, we will have biased estimators on \(\theta\). To avoid this problem, we can use nonparametric estimation. The starting point for a density estimation is a histogram. We define the intervals by choosing a number of bins and a starting value for the first interval. Here, we use 0 as a starting value and 10 bins:

#Random integers from 1 to 100
set.seed(123)
data <- sample(1:100, 100, replace = TRUE)
stem(data)

## 
##   The decimal point is 1 digit(s) to the right of the |
## 
##   0 | 46777999
##   1 | 23344456
##   2 | 12335555677
##   3 | 00111224456889
##   4 | 01122337
##   5 | 0012337
##   6 | 003477999
##   7 | 1222466899
##   8 | 112366799
##   9 | 0011123334566799

foo <- hist(data, nclass = 10,
            col = "lightblue",
            cex.main = 0.80, cex.axis = 0.75)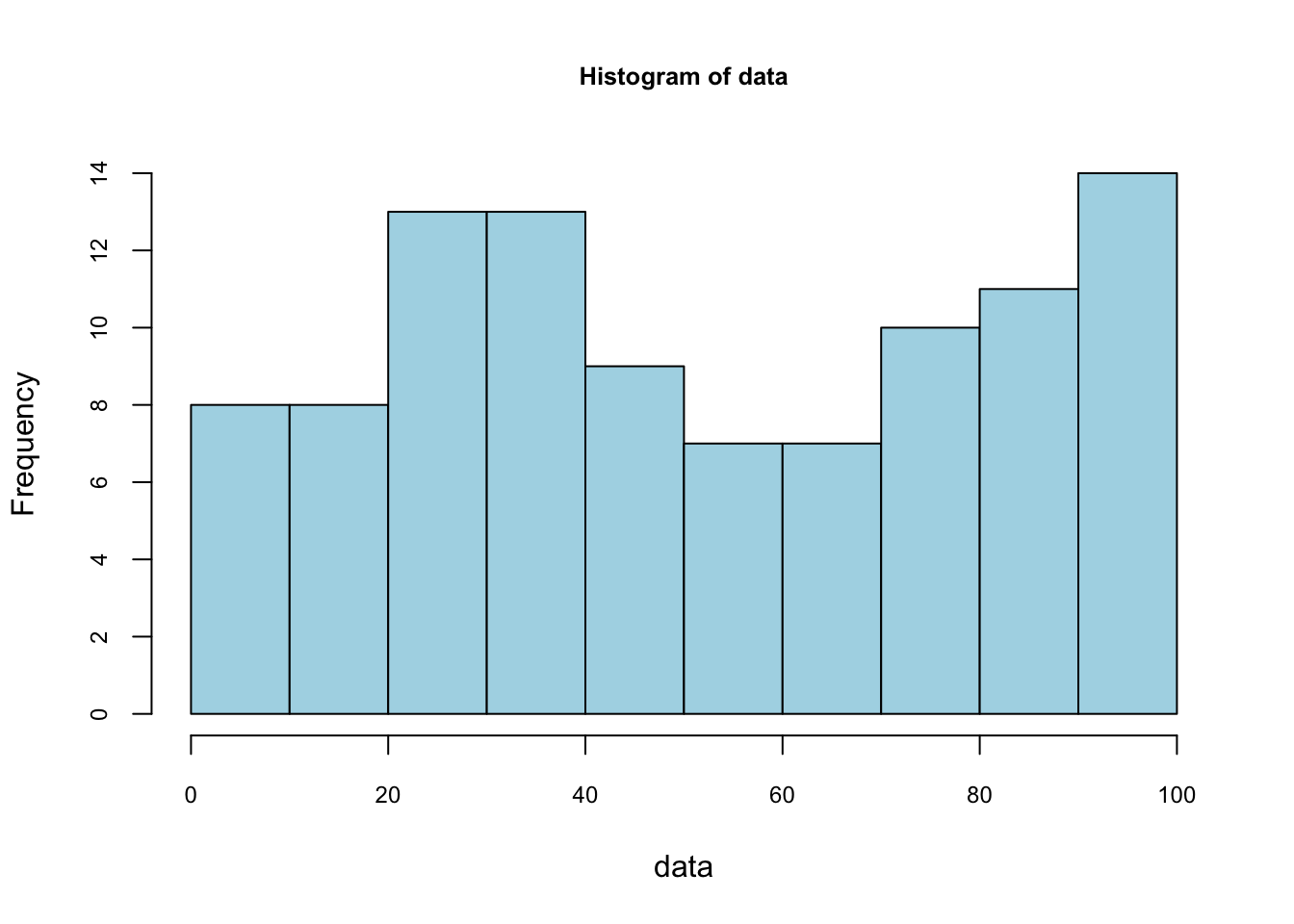

foo$counts

##  [1]  8  8 13 13  9  7  7 10 11 14

foo$density

##  [1] 0.008 0.008 0.013 0.013 0.009 0.007 0.007 0.010 0.011 0.014

sum(foo$density)

## [1] 0.1

Not that the sum of these densities is not one. The vertical scale of a ‘frequency histogram’ shows the number of observations in each bin. From above, we know that the tallest bar has 14 observations, so this bar accounts for relative frequency 14/100=0.14 of the observations. As the relative frequency indicate probability their total would be 1. We are looking for a density function which gives the “height” of each observation. Since the width of this bar is 10, the density of each observation in the bin is 0.014.

Can we have a formula that we calculate the density for each bin?

\[\begin{equation} \hat{f}(y)=\frac{1}{n} \times \frac{\text{ number of observations in the interval of } y}{\text { width of the interval }} \tag{6.3} \end{equation}\]

Here is the pdf on the same data with binwidth = 4 for our example:

# to put pdf and X's on the same graph, we scale the data
foo <- hist(data/(10*mean(data)), nclass = 25,
            cex.main = 0.80, cex.axis = 0.75, xlim = c(0, 0.2))
lines(foo$mids, foo$density, col="blue", lwd = 2) #Naive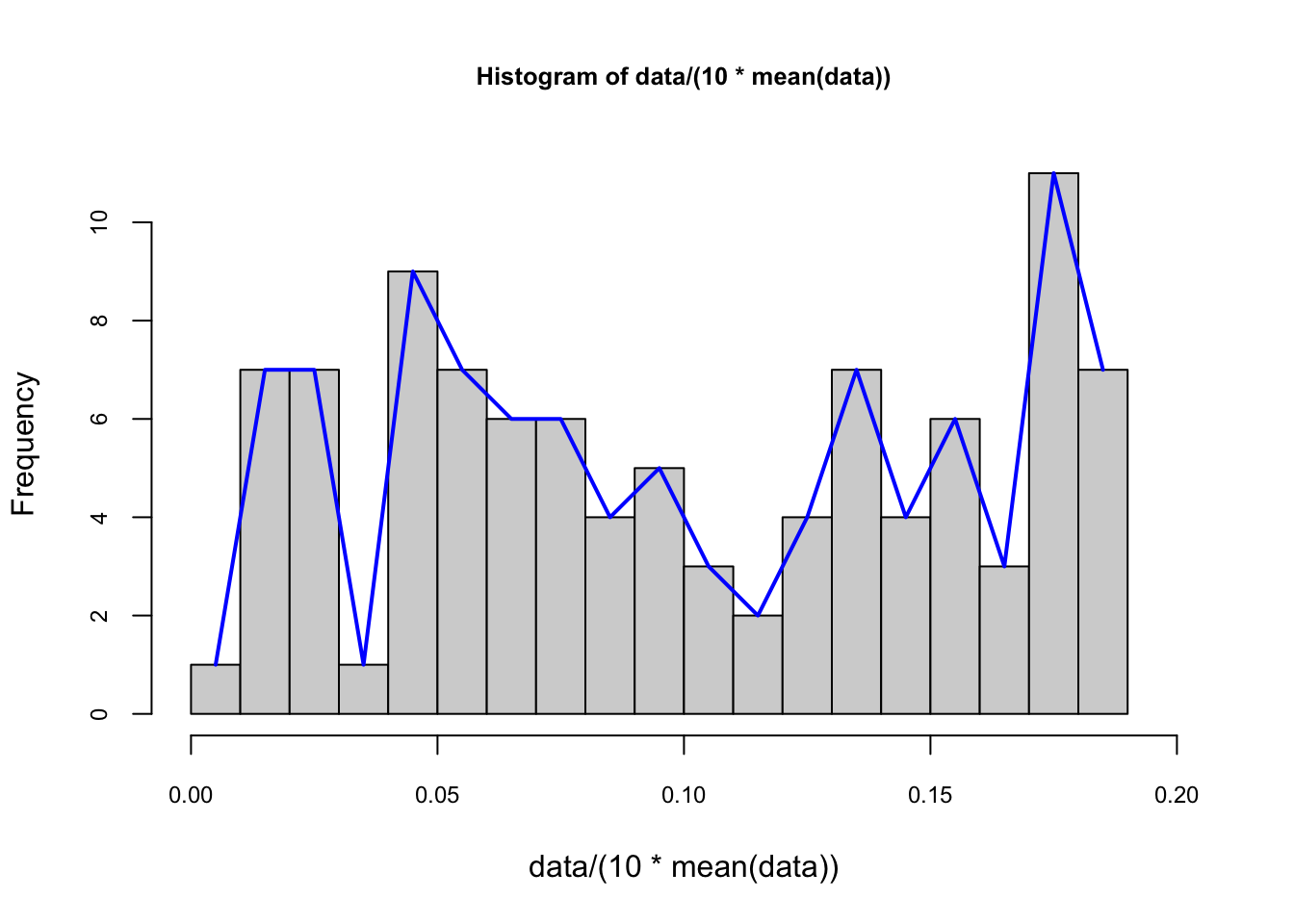

The number of bins defines the degree of smoothness of the histogram. We can have the following general expression for a nonparametric density estimation:

\[\begin{equation} f(x) \cong \frac{k}{n h} \text { where }\left\{\begin{array}{ll}{h} & {\text { binwidth }} \\ {n} & {\text { total } \text { number of observation points }} \\ {k} & {\text { number of observations inside } h}\end{array}\right. \tag{6.4} \end{equation}\]

Note that, in practical density estimation problems, two basic approaches can be adopted: (1) we can fix \(h\) (width of the interval) and determine \(k\) in each bin from the data, which is the subject of this chapter and called kernel density estimation (KDE); or (2) we can fix \(k\) in each bin and determine \(h\) from the data. This gives rise to the k-nearest-neighbors (kNN) approach, which we cover in the next chapters.

The global density is obtained with a moving window (intervals with intersections). This also called as Naive estimator (a.k.a. Parzen windows), which is not sensitive to the position of bins, but it is not smooth either. We can rewrite it as

\[\begin{equation} \hat{f}(y)=\frac{1}{n h} \sum_{i=1}^{n} I\left(y-\frac{h}{2}<y_{i}<y+\frac{h}{2}\right), \tag{6.5} \end{equation}\]

where \(I(.)\) is an indicator function, which results in value of 1 if the expression inside of the function is satisfied (0 otherwise). Hence it counts the number of observations in a given window. The binwidth (\(h\)) defines the bin range by adding and subtracting \(h/2\) from \(y\). Let’s rearrange 6.5 differently:

\[ \hat{f}(y)=\frac{1}{2n h} \sum_{i=1}^{n} I\left(y-h<y_{i}<y+h\right) \]

If we rewrite the inequality by subtracting \(y\) and divide it by \(h\):

\[ \hat{f}(y)=\frac{1}{2n h} \sum_{i=1}^{n} I\left(-1<\frac{y-y_{i}}{h}<1\right) \] which can be written more compactly,

\[\begin{equation} \hat{f}(y)=\frac{1}{2nh} \sum_{i=1}^{n} w\left(\frac{y-y_{i}}{h}\right) \quad \text { where } \quad w(x)=\left\{\begin{array}{ll}{1} & {\text { if }|x|<1} \\ {0} & {\text { otherwise }}\end{array}\right. \tag{6.6} \end{equation}\]

Consider a sample \(\left\{X_{i}\right\}_{i=1}^{10}\), which is 4, 5, 5, 6, 12, 14, 15, 15, 16, 17. And the bin width is \(h=4\). What’s the density of 3, i.e, \(\hat{f}(3)\)? Note that there is not 3 in the data.

\[ \begin{aligned} \hat{f}(3) &=\frac{1}{2*10*4}\left\{w\left(\frac{3-4}{4}\right)+w\left(\frac{3-5}{4}\right)+\ldots+w\left(\frac{3-17}{4}\right)\right\} \\ &=\frac{1}{80}\left\{1+1+1+1+0+\ldots+0\right\} \\ &=\frac{1}{20} \end{aligned} \]

This “naive” estimator yields density estimates that have discontinuities and weights equal at all points \(x_i\) regardless of their distance to the estimation point \(x\). In other words, in any given bin, \(x\)’s have a uniform distribution. That’s why, \(w(x)\) is commonly replaced with a smooth kernel function \(K(x)\). Kernel replaces it with usually, but not always, with a radially symmetric and unimodal pdf, such as the Gaussian. You can choose “gaussian”, “epanechnikov”, “rectangular”, “triangular”, “biweight”, “cosine”, “optcosine” distributions in the R’s density() function. With the Kernel density estimator replacing \(w\) by a kernel function \(K\):

\[\begin{equation} \hat{f}(y)=\frac{1}{2n h} \sum_{i=1}^{n} K\left(\frac{y-y_{i}}{h}\right), \tag{6.7} \end{equation}\]

Here are the samples of kernels, \(K(x)\):

\[ \text { Rectangular (Uniform): } ~~ K(x)=\left\{\begin{array}{ll}{\frac{1}{2}} & {|x|<1} \\ {0} & {\text { otherwise }}\end{array}\right. \] \[ \text { Epanechnikov: } ~~ K(x)=\left\{\begin{array}{cc}{\frac{3}{4}\left(1-\frac{1}{5} x^{2}\right) / \sqrt{5}} & {|x|<\sqrt{5}} \\ {0} & {\text { otherwise }}\end{array}\right. \] \[ \text { Gaussian: } ~~ K(x)=\frac{1}{\sqrt{2 \pi}} e^{(-1 / 2) x^{2}} \]

Although the kernel density estimator depends on the choices of the kernel function \(K\), it is very sensitive to \(h\), not to \(K\).

In R, the standard kernel density estimation is obtained by density(), which uses Silverman rule-of-thumb to select the optimal bandwidth, \(h\), and the Gaussian kernel. Here is an example with our artificial data:

X <- readRDS("fes73.rds")
X <- X/mean(X)
hist(X[X<3.5], nclass = 130 , probability = TRUE, col = "white",
     cex.axis = 0.75, cex.main = 0.8)
lines(density(X, adjust = 1/4), col = "red") # bw/4
lines(density(X, adjust = 1), col = "blue") # bw
lines(density(X, adjust = 4), col = "green") # bw * 4
lines(density(X, kernel = "rectangular", adjust = 1/4), col = "black") # bw * 4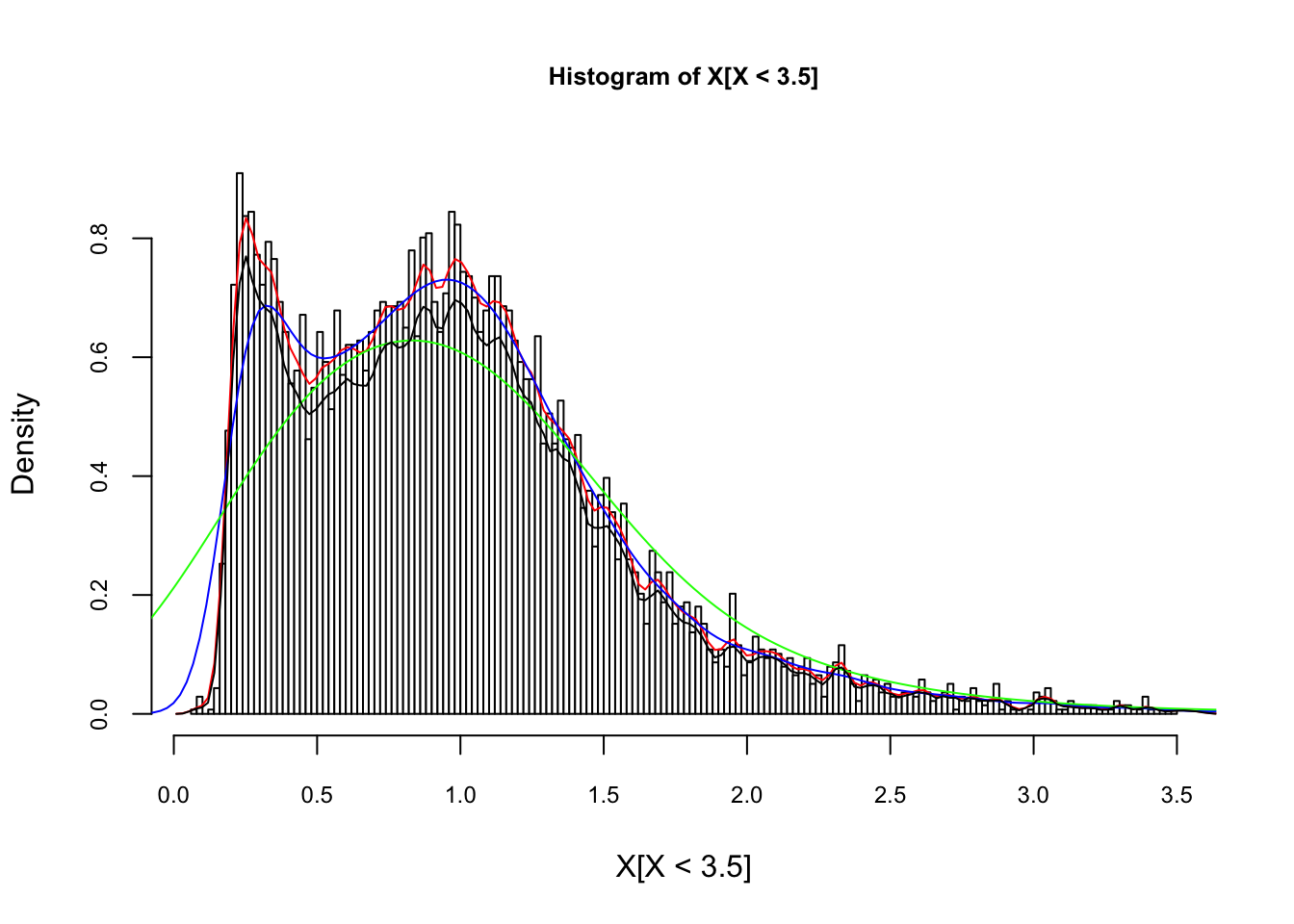

#Here is the details of the last one
density(X, adjust = 4)

## 
## Call:
##  density.default(x = X, adjust = 4)
## 
## Data: X (6968 obs.); Bandwidth 'bw' = 0.3423
## 
##        x                y            
##  Min.   :-0.954   Min.   :0.0000000  
##  1st Qu.: 2.352   1st Qu.:0.0000576  
##  Median : 5.657   Median :0.0005510  
##  Mean   : 5.657   Mean   :0.0755509  
##  3rd Qu.: 8.963   3rd Qu.:0.0269050  
##  Max.   :12.269   Max.   :0.6282958

Bigger the bandwidth \(h\) smoother the pdf. Which one is better? Here, we again have a bias-variance tradeoff. As we will see later, \(h\) can be found by cross-validation methods. An example of cross-validation methods on KDE can be found here (García-Portugués 2022b).

Why do we estimate pdf with KDE? Note that, when you explore our density object by str(), you’ll see that \(Y\) will get you the pdf values of density for each value of \(X\) you have in our data. Of course pdf is a function: the values of pdf are \(Y\) and the input values are \(X\). Hence, given a new data point on \(X\), we may want to find the outcome of \(Y\) (the value of pdf for that data point) based on the function, the kernel density estimator that we have from the density() function result. How can we do that? Lets look at an example.

poo <- density(X, adjust = 4)

dens <- with(poo, approxfun(x, y, rule=1))
# Here y is the pdf of a specified x.
dens(1.832)

## [1] 0.2036082

This is a predicted value of pdf when \(x=1.832\) estimated by KDE without specifying the model apriori, which is like a magic! Based on the sample we have, we just predicted \(Y\) without explicitly modeling it. Keep in mind that our objective here is not to estimate probabilities. We can do it if we want. But then, of course we have to remember that values of a density curve are not the same thing as probabilities. As with any continuous distribution, the probability that \(X\) is exactly 1.832, for example, is 0. Taking the integral of the desired section in the estimated pdf would give us the corresponding probability.

6.2 Kernel regressions

Theoretically, nonparametric density estimation can be easily extended to several dimensions (multivariate distributions). For instance, suppose you are interested in the relationship between one endogenous variable \(Y\) and a few exogenous variables of \(X\). The ultimate goal is forecasting new realizations of \(Y\) given new realizations of \(X\)’s. You have little clue what functional form the relationship could take. Suppose you have a sufficiently large sample, so that you may obtain a reasonably accurate estimate of the joint probability density (by kernel density estimation or similar) of \(Y\) and the \(X\)’s.

In practice, however, you rarely actually have a good enough sample to perform highly accurate density estimation. As the dimension increases, KDE rapidly needs many more samples. Hence, KDE is rarely useful beyond the order of 10 dimensions. Even in low dimensions, a density estimation-based model has essentially no ability to generalize; if your test set has any examples outside the support of your training distribution, you’re likely in trouble.

In regression functions, the outcome is the conditional mean of \(Y\) given \(X\)’s. Unlike linear regression, nonparametric regression is agnostic about the functional form between the outcome and the covariates and is therefore not subject to misspecification error. In nonparametric regression, you do not specify the functional form. You specify the outcome variable and the covariates. In traditional parametric regression models, the functional form of the model is specified before the model is fit to data, and the objective is to estimate the parameters of the model. In nonparametric regression, in contrast, the objective is to estimate the regression function directly without specifying its form explicitly ².

The traditional regression model fits the model:

\[\begin{equation} y=m(\mathbf{x}, \boldsymbol{\theta})+\varepsilon \tag{6.8} \end{equation}\]

where \(\theta\) is a vector of parameters to be estimated, and x is a vector of predictors. The errors, \(\varepsilon\) are assumed to be normally and independently distributed with mean 0 and constant variance \(\sigma^2\). The function \(m(\mathbf{x},\theta)\), relating the average value of the response \(y\) to the predictors, is specified in advance, as it is in a linear regression model. The general nonparametric regression model is written in a similar manner, but the function \(m\) is left unspecified for the \(p\) predictors:

\[ \begin{aligned} y &=m(\mathbf{x})+\varepsilon \\ &=m\left(x_{1}, x_{2}, \ldots, x_{p}\right)+\varepsilon \end{aligned} \] Moreover, the objective of nonparametric regression is to estimate the regression function \(m(\mathbf{x})\) directly, rather than to estimate parameters. Most methods of nonparametric regression implicitly assume that \(m\) is a smooth, continuous function. As in nonlinear regression, it is standard to assume that error is normally and identically distributed \(\varepsilon \sim NID(0, \sigma^2)\).

An important special case of the general model is nonparametric simple regression, where there is only one predictor:

\[ y=m(x)+\varepsilon \]

Because it is difficult to fit the general nonparametric regression model when there are many predictors, and because it is difficult to display the fitted model when there are more than two or three predictors, more restrictive models have been developed. One such model is the additive regression model,

\[\begin{equation} y=\beta_{0}+m_{1}\left(x_{1}\right)+m_{2}\left(x_{2}\right)+\cdots+m_{p}\left(x_{p}\right)+\varepsilon \tag{6.9} \end{equation}\]

Variations on the additive regression model include semiparametric models, in which some of the predictors enter linearly or interactively.³

Let’s consider the simplest situation with one continuous predictor, \(X\). Due to its definition, we can rewrite \(m\) as

\[\begin{equation} \begin{split} \begin{aligned} m(x) &=\mathbb{E}[Y | X=x] \\ &=\int y f_{Y | X=x}(y) \mathrm{d} y \\ &=\frac{\int y f(x, y) \mathrm{d} y}{f_{X}(x)} \end{aligned} \end{split} \tag{6.10} \end{equation}\]

This shows that the regression function can be computed from the joint density \(f(x,y)\) and the marginal \(f(x)\). Therefore, given a sample \(\left\{\left(X_{i}, Y_{i}\right)\right\}_{i=1}^{n}\), a nonparametric estimate of \(m\) may follow by replacing the previous densities by their kernel density estimators, which we’ve just seen in the previous section.

A limitation of the bin smoothing approach in kernel density estimations is that we need small windows for the approximately constant assumptions to hold. As a result, we end up with a small number of data points to average and obtain imprecise estimates of \(f(x)\). Local weighted regression (loess) permits us to consider larger window sizes. loess() is a nonparametric approach that fits multiple regressions in local neighborhood. It is called local regression because, instead of assuming the function is approximately constant in a window, it fits a local regression at the “neighborhood” of \(x_0\). The distance from \(x_0\) is controlled by the span setting, which determines the width of the moving (sliding) window when smoothing the data. span (also defined as alpha) represents the proportion of the data (size of the sliding window) that is considered to be neighboring \(x_0\) ⁴. Moreover, the weighting in the regression is proportional to \(1-(\text{distance}/\text{maximum distance})^3)^3\), which is called the Tukey tri-weight. Different than the Gaussian kernel, the Tukey tri-weight covers more points closer to the center point.

We will not see the theoretical derivations of kernel regressions but an illustration of local polynomial of order 0, 1 and 2, below. (Examples from Ahamada and Flachaire) (2011). The Nadaraya–Watson estimator is a local polynomial of order 0, which estimates a local mean of \(Y_1...Y_n\) around \(X=x_0\).

#Simulating our data
n = 300
set.seed(1)
x <- sort(runif(n)*2*pi)
y <- sin(x) + rnorm(n)/4
plot(x, y)

#Estimation
loe0 <- loess(y~x, degree=0, span = 0.5) #Nadaraya-Watson
loe1 <- loess(y~x, degree=1, span = 0.5) #Local linear
loe2 <- loess(y~x, degree=2, span = 0.5) #Locally quadratic

#To have a plot, we first calculate the fitted values on a grid,
t <- seq(min(x), max(x), length.out = 100)
fit0 <- predict(loe0, t)
fit1 <- predict(loe1, t)
fit2 <- predict(loe2, t)
plot(x, y, col = "gray", cex.main = 0.80, cex.axis = 0.75)
lines(t, fit0, col = "green", lwd = 3)
lines(t, fit1, col = "red")
lines(t, fit2, col = "blue")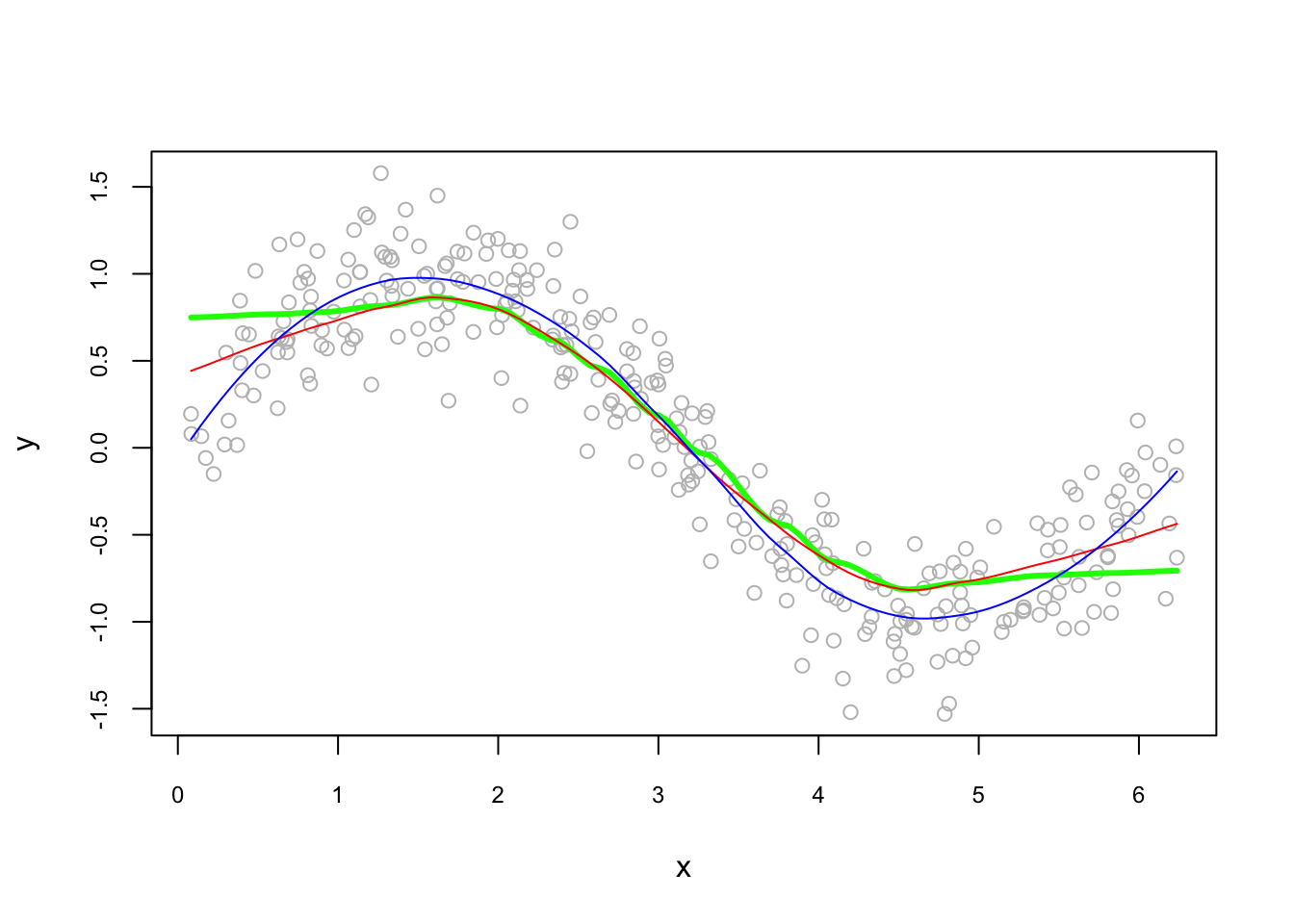

Let’s see sensitivity of local quadratic to the bandwidth:

fit0 <- predict(loess(y~x, degree=2, span = 0.05)) #minimum, 5%*300 = 14 obs. 
fit1 <- predict(loess(y~x, degree=2, span = 0.75)) #default
fit2 <- predict(loess(y~x, degree=2, span = 2)) 

plot(x, y, col = "gray", cex.main = 0.80, cex.axis = 0.75)
lines(x, fit0, lwd = 2, col = "green")
lines(x, fit1, lwd = 2, col = "red")
lines(x, fit2, lwd = 2, col = "blue")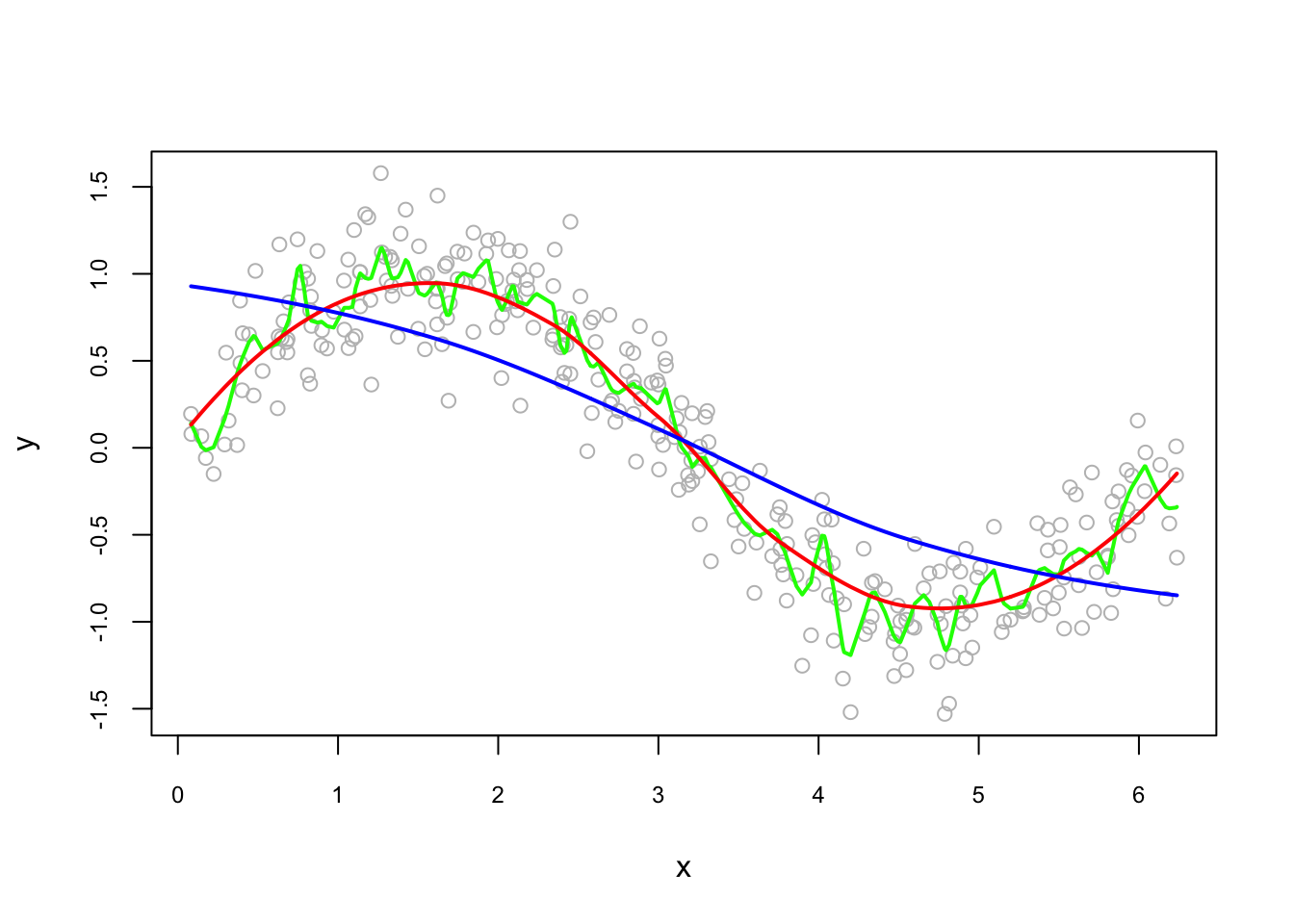

As we have seen in the concept of bias-variance trade off before, which bandwidth we choose will be determined by the prediction accuracy. This subject is related to cross-validation, which we will see later as a whole chapter.

6.3 Regression Splines

In a model, non-linearity can be captured by estimating a linear regression through several intervals, which is called as piecewise linear model.

\[\begin{equation} \begin{split} \begin{array}{ll}{y=\alpha_{1}+\beta_{1} x+\varepsilon_{1}} & {\text { if } \quad x \in\left[z_{0} ; z_{1}\right]} \\ {y=\alpha_{2}+\beta_{2} x+\varepsilon_{2}} & {\text { if } \quad x \in\left[z_{1} ; z_{2}\right]} \\ {\cdots} \\ {y=\alpha_{k}+\beta_{k} x+\varepsilon_{k}} & {\text { if } \quad x \in\left[z_{k-1} ; z_{k}\right]}\end{array} \end{split} \tag{6.11} \end{equation}\]

However, the function is not smoothed at the knots, \(z.\) Hence, regression spline is a piecewise regression model with a smooth transition at the knots. Further, smoothing spline is to reduce the influence of the number of knots chosen, the criterion function is penalized.

First, let’s see how a piecewise regression works with an example. To show evidence of nonlinearity between short and long-term interest rates, Pfann et al (1996) estimates the following piecewise linear model:

\[\begin{equation} y=\beta_{0}+\beta_{1} x+\beta_{2}(x-\kappa)_{+}+\varepsilon \tag{6.12} \end{equation}\]

Here in 6.12 the \(\kappa\) is called as knot where the relationship between \(Y\) and \(x\) changes. (Subscript \(+\) means that the term will be zero when it is not positive).

data <- read.table("irates.dat", header = TRUE)
y <- data$GS10
x <- data$TB3MS
xk <- (x - 10.8)*(x > 10.8)
summary(lm(y ~ x + xk))

## 
## Call:
## lm(formula = y ~ x + xk)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -2.3978 -0.9051 -0.1962  0.9584  3.2530 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.77900    0.10181   17.47  < 2e-16 ***
## x            0.92489    0.01915   48.29  < 2e-16 ***
## xk          -0.42910    0.08958   -4.79 2.06e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.107 on 657 degrees of freedom
## Multiple R-squared:   0.83,  Adjusted R-squared:  0.8295 
## F-statistic:  1604 on 2 and 657 DF,  p-value: < 2.2e-16

reorder <- order(x) # to avoid messy lines
plot(x[reorder], fitted(lm(y ~ x + xk))[reorder], type="l", col = "red",
     cex.main = 0.80, cex.axis = 0.75, xlab = "TB3MS", ylab = "GS10")
points(x, y, col = "grey")
abline(v = 10.8, lty = 2, col = "darkgreen")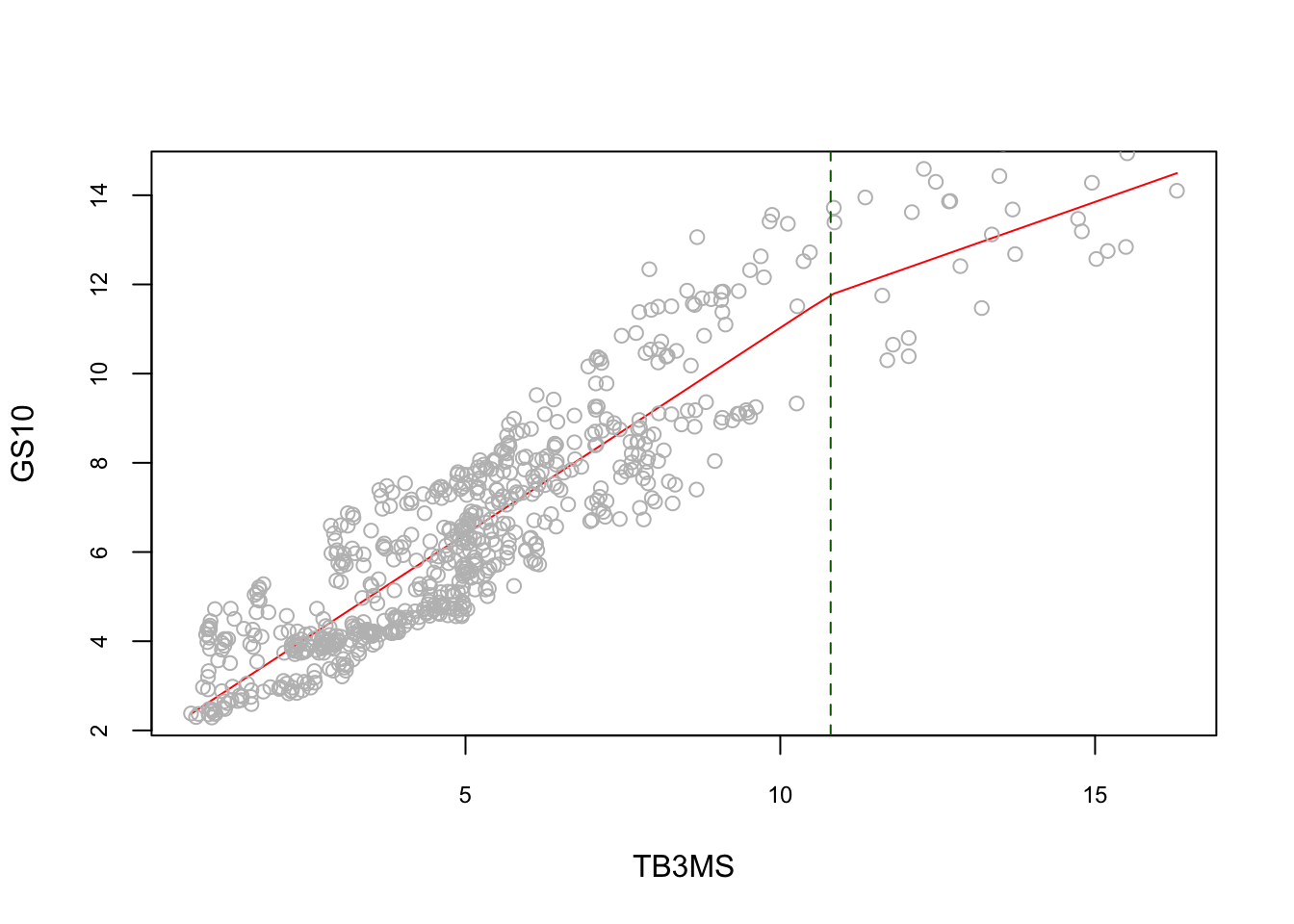

When the model is extended to \(q\) knots, it becomes a piecewise regression:

\[\begin{equation} y=\beta_{0}+\beta_{1} x+\sum_{j=1}^{q} \beta_{1 j}\left(x-\kappa_{j}\right)_{+}+\varepsilon \tag{6.13} \end{equation}\]

#5 knots
k <- c(2.8, 4.8, 6.8, 8.8, 10.8)
Xk <- x - matrix(k, NROW(x), NROW(k), byrow = TRUE)

#nrow and ncol return the number of rows or columns present in a matrix.
#NCOL and NROW do the same treating a vector as 1-column matrix.
#Try these: nrow(x) and NROW(x) to see the difference.
#you can use lenght() instead of NROW/NCOL in vectors, though.

Xk <- Xk*(Xk > 0)

reorder <- order(x) # to avoid messy lines
plot(x, y, col = "gray", ylim = c(2.5, 14.5),
     cex.main = 0.80, cex.axis = 0.75, xlab = "TB3MS", ylab = "GS10")
lines(x[reorder], fitted(lm(y ~ x + Xk))[reorder], lwd = 2, col = "red")
abline(v = k, lty = 2, col = "darkgreen")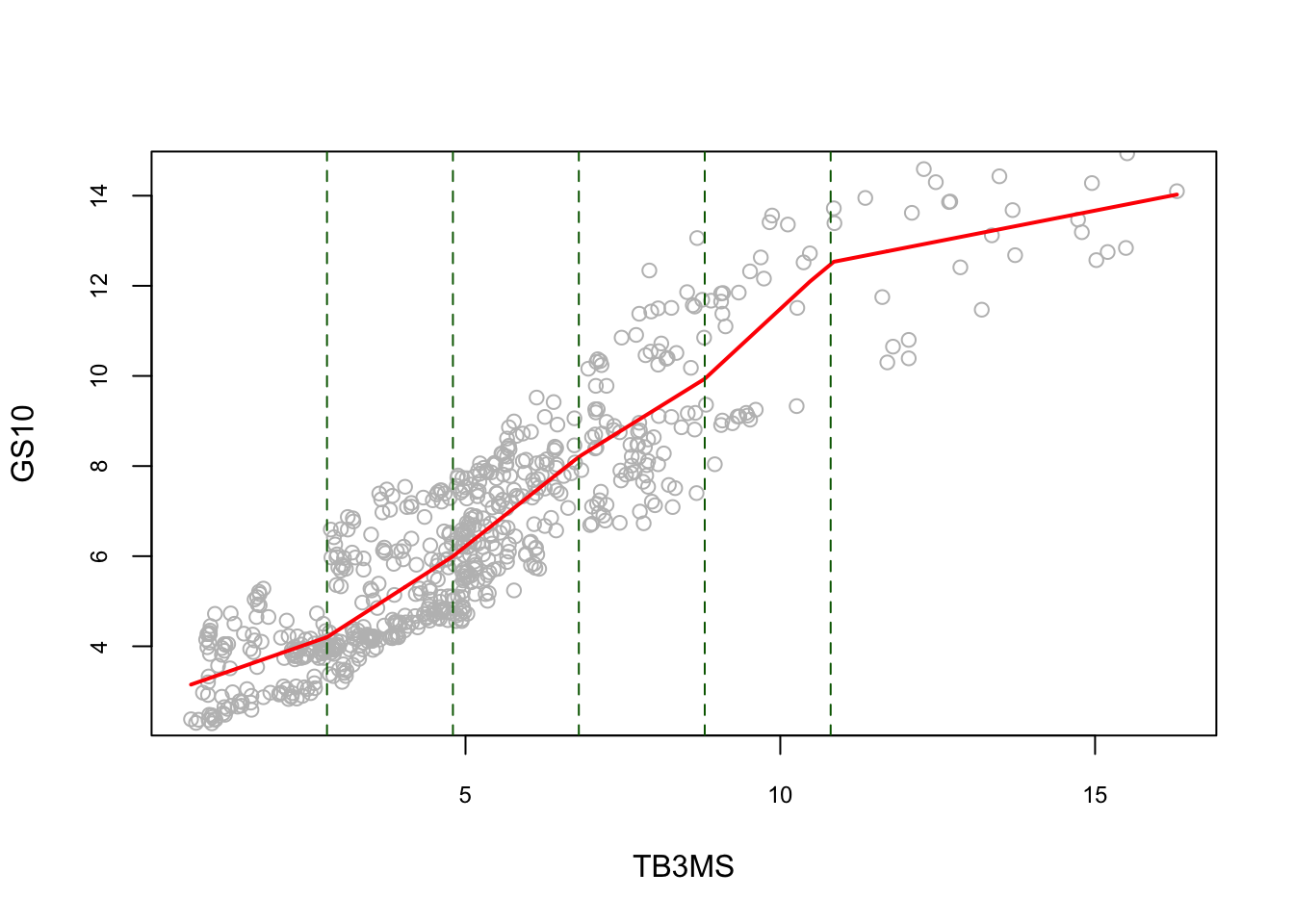

The piecewise linear model is not smooth at the knots. To get a smooth estimator, we replace the basis of linear functions by a basis of spline functions, which is defined as

\[ b_{0}(x, \kappa), \ldots, b_{r}(x, \kappa) \] Hence, regression spline is defined as:

\[\begin{equation} y=\sum_{j=0}^{r} \beta_{j} b_{j}(x, \kappa)+\varepsilon \tag{6.14} \end{equation}\]

Hence, once the knots are fixed, it becomes essentially a parametric regression. For example, spline regression model at order \(p\) can be expressed as

\[ y=\beta_{0}+\beta_{1} x+\cdots+\beta_{p} x^{p}+\sum_{j=1}^{q} \beta_{p j}\left(x-\kappa_{j}\right)_{+}^{p}+\varepsilon \]

Suppose that an estimation with cubic splines gives:

\[ \hat{m}(x)=2+x-2 x^{2}+x^{3}+(x-0.4)_{+}^{3}-(x-0.8)_{+}^{3} \]

It means that coordinates of \(y\) in the basis of cubic splines are (2; 1;-2; 1; 1;-1), with knots 0:4 and 0:8. This estimation can be rewritten:

\[ \hat{m}(x)=\left\{\begin{aligned} 2+x-2 x^{2}+x^{3} & \text { if } & x<0.4 \\ 2+x-2 x^{2}+x^{3}+(x-0.4)^{3} & \text { if } & 0.4 \leq x<0.8 \\ 2+x-2 x^{2}+x^{3}+(x-0.4)^{3}-(x-0.8)^{3} & \text { if } & x \geq 0.8 \end{aligned}\right. \]

In short a spline is a piecewise polynomial function. Now the question is how we are supposed to choose the basis and the knots? For the knots, spline estimation is sensitive to the choice of the number of knots and their position. A knot can have an economic interpretation such as a specific date or structural change in the data, thus some information is required. There are two common approaches for choosing the position of the knots: quantiles - intervals with the same number of observations and equidistant - intervals with the same width. As for the number of knots, if it’s too small, the potential bias can be large in the estimator, so a larger number is preferred.

Let’s use the same data and apply regression spline. Here is the example for equidistant knots:

library(splines)

#equidistant knots
nknots <- 5
k = seq(min(x), max(x), length.out = nknots + 2)[2:(nknots + 1)]
model1 <- lm(y ~ bs(x, degree = 3, knots = k)) #check ?bs
#Generate the B-spline basis matrix for a polynomial spline.
summary(model1)

## 
## Call:
## lm(formula = y ~ bs(x, degree = 3, knots = k))
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -2.5190 -0.8537 -0.1889  0.8841  3.2169 
## 
## Coefficients:
##                               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                     3.1855     0.3160  10.082  < 2e-16 ***
## bs(x, degree = 3, knots = k)1   0.4081     0.5722   0.713  0.47596    
## bs(x, degree = 3, knots = k)2   0.9630     0.3163   3.045  0.00242 ** 
## bs(x, degree = 3, knots = k)3   4.2239     0.4311   9.798  < 2e-16 ***
## bs(x, degree = 3, knots = k)4   6.2233     0.3869  16.084  < 2e-16 ***
## bs(x, degree = 3, knots = k)5   9.9021     0.6620  14.957  < 2e-16 ***
## bs(x, degree = 3, knots = k)6   9.8107     0.8370  11.722  < 2e-16 ***
## bs(x, degree = 3, knots = k)7  10.8604     0.9400  11.553  < 2e-16 ***
## bs(x, degree = 3, knots = k)8  10.6991     1.0866   9.847  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.086 on 651 degrees of freedom
## Multiple R-squared:  0.8378, Adjusted R-squared:  0.8358 
## F-statistic: 420.3 on 8 and 651 DF,  p-value: < 2.2e-16

u <- seq(min(x), max(x), length.out = 100)
pred <- predict(model1, newdata = list(x=u), se = TRUE) #see ?predict for arguments

reorder <- order(u) # to avoid messy lines
plot(x, y, col = "gray", ylim = c(2.5, 14.5),
     cex.main = 0.80, cex.axis = 0.75)
lines(u, pred$fit, lwd = 2, col = "red")
lines(u[reorder], pred$fit[reorder] + 1.96*pred$se, lty = "dashed")
lines(u[reorder], pred$fit[reorder] - 1.96*pred$se, lty = "dashed")
abline(v = k, lty = 2, col = "darkgreen")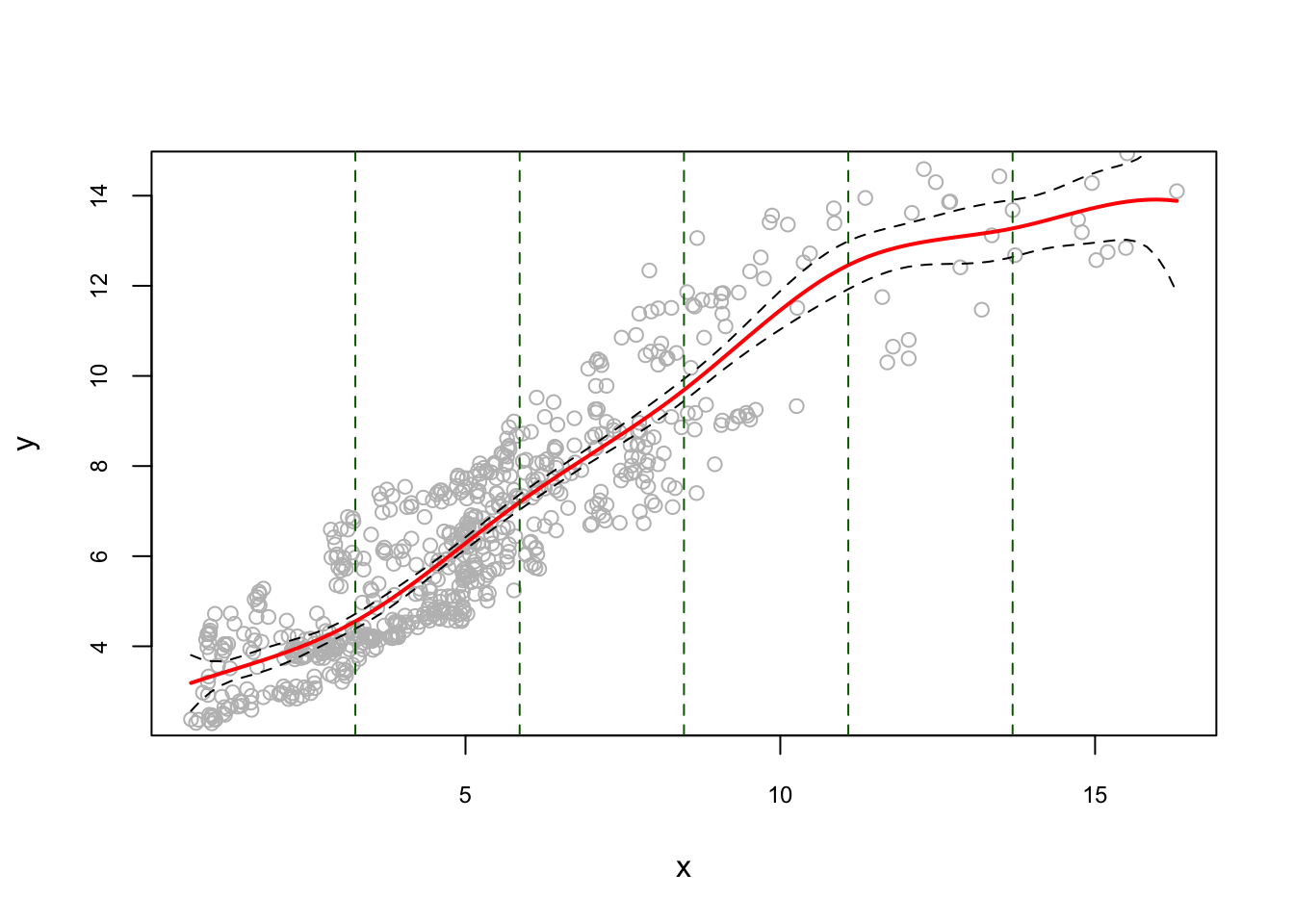

And, an example for quantile knots:

model2 <- lm(y ~ bs(x, degree = 3, df = 8))
#In regression spline, df (degree of freedom)
#is the number of components of the basis. Thus,
#with cubic spline, df=6 defines 3 knots (quartiles q:25; q:5; q:75)
#Since we have df= 8, we have 5 knots, so is the quantile of 20%
u <- seq(min(x), max(x), length.out = 100)
pred <- predict(model2, newdata = list(x=u), se = TRUE) #see ?predict for arguments

reorder <- order(u) # to avoid messy lines
plot(x, y, col = "gray", ylim = c(2.5, 14.5),
     cex.main = 0.80, cex.axis = 0.75)
lines(u, pred$fit, lwd = 2, col = "red")
lines(u[reorder], pred$fit[reorder] + 1.96*pred$se, lty = "dashed")
lines(u[reorder], pred$fit[reorder] - 1.96*pred$se, lty = "dashed")
k <- attr(bs(x, degree = 3, df = 8), "knots") 
#These functions provide access to a single attribute of an object.
abline(v = k, lty = 2, col = "darkgreen")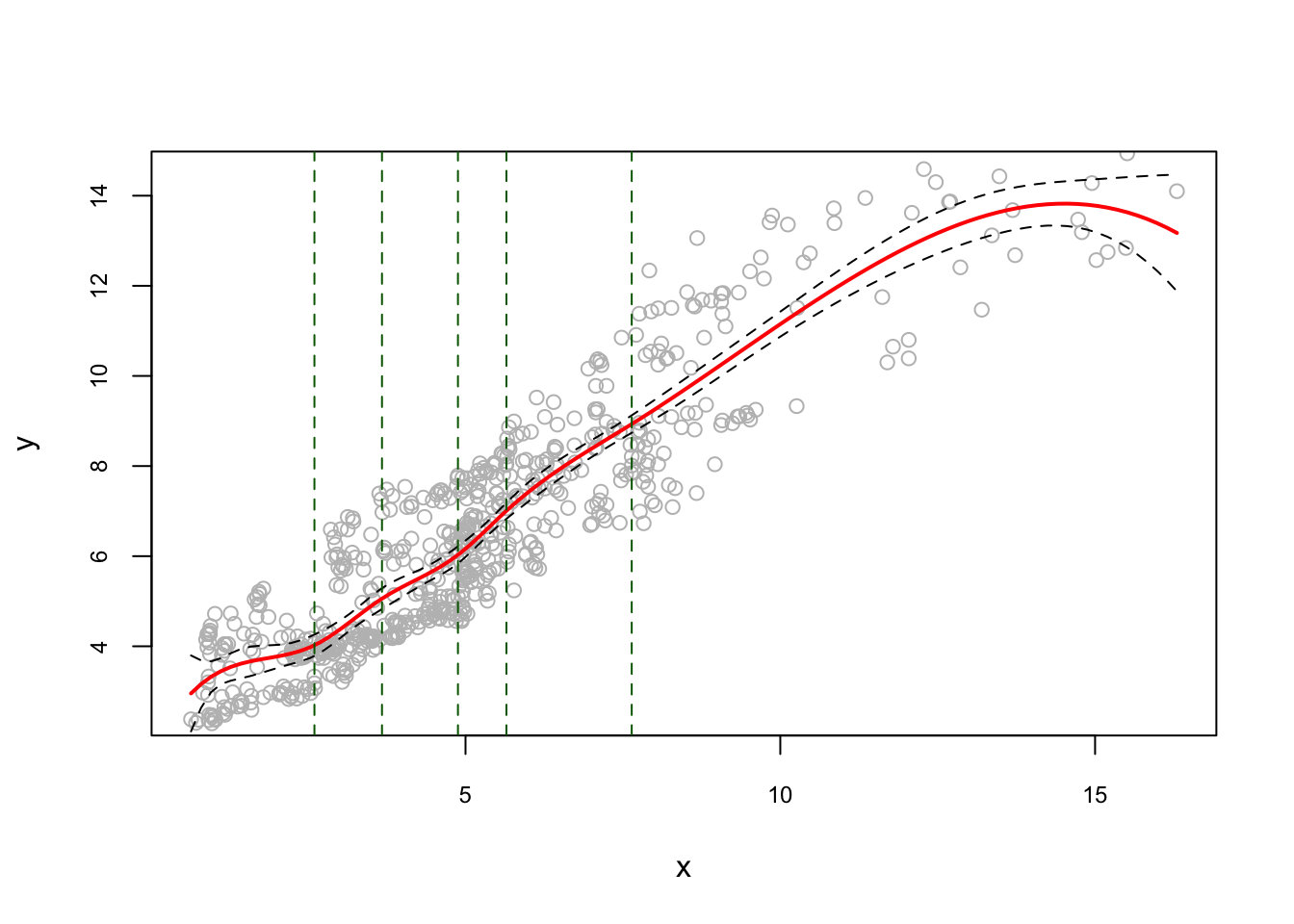

Is bad or good for prediction to have a very large number of knots? See https://freakonometrics.hypotheses.org/47681 (Charpentier 2016), for the argument about the number of knots. Here is Arthur Charpentier’s conclusion:

So, it looks like having a lot of non-significant components in a spline regression is not a major issue. And reducing the degrees of freedom is clearly a bad option.

Let’s see how sensitive the results to the number of knots ⁵:

pred1 <- predict(lm(y ~ bs(x, degree = 3, df = 6)))   #quartiles
pred2 <- predict(lm(y ~ bs(x, degree = 3, df = 12)))  #deciles
pred3 <- predict(lm(y ~ bs(x, degree = 3, df = 102))) #percentile

reorder <- order(x) 
plot(x, y, col = "gray", ylim = c(2.5, 14.5),
     cex.main = 0.80, cex.axis = 0.75)
lines(x[reorder], pred1[reorder], lwd = 2, col = "red")
lines(x[reorder], pred2[reorder], lwd = 2, col = "blue")
lines(x[reorder], pred3[reorder], lwd = 2, col = "green")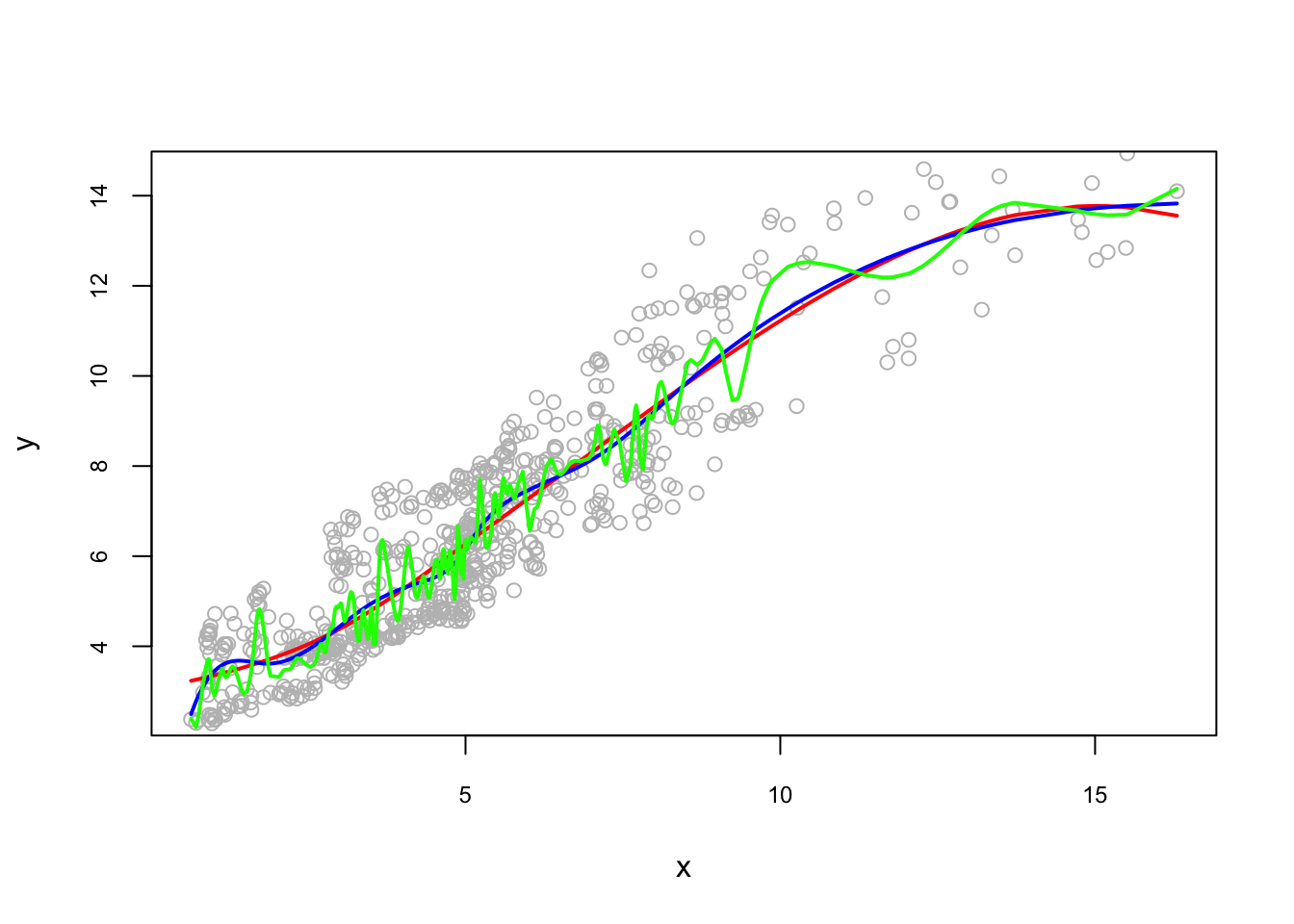

There is a method called as smoothing spline, a spline basis method that avoids the knot selection problem. It uses a maximal set of knots, at the unique values of the each \(X\) values and control for the fit by regularization. Similar to OLS, it selects \(\beta_j\) to minimize the residual sum of squares but with a penalization on the curvature in the function:

\[\begin{equation} \sum_{i=1}^{n}\left[y_{i}-m\left(x_{i}\right)\right]^{2}+\lambda \int\left[m^{\prime \prime}(x)\right]^{2} d x \tag{6.15} \end{equation}\]

The first term minimizes the closeness to the data with a constraint (the second term) on the curvature in the function. If \(\lambda=0\), \(m(x_i)\) could be any function that fits the data very closely (interpolates the data). If \(\lambda > 0\) and goes infinity, it makes the penalization so high that the algorithm fits a simple least squares line without any curvature. The penalty term, or bandwidth \(\lambda\), restricts fluctuations of \(\hat{m}\) and the optimum \(\lambda\) minimizes the distance between \(m\), which is unknown, and \(\hat{m}\). The method used to find the optimal \(\lambda\) is called as generalized cross-validation. Here is a simulation:

set.seed(1)
n <- 200
x <- runif(n)
dgm <- sin(12*(x + 0.2))/(x + 0.2) # our dgm
y <- dgm + rnorm(n)
plot(x, y, col = "gray", cex.main = 0.80, cex.axis = 0.75)

lines(x[order(x)], dgm[order(x)], lwd = 2, col = "black") # DGM
lines(smooth.spline(x,y, df = 20), lwd = 2, col = "red")
lines(smooth.spline(x,y, df = 40), lwd = 2, col = "blue")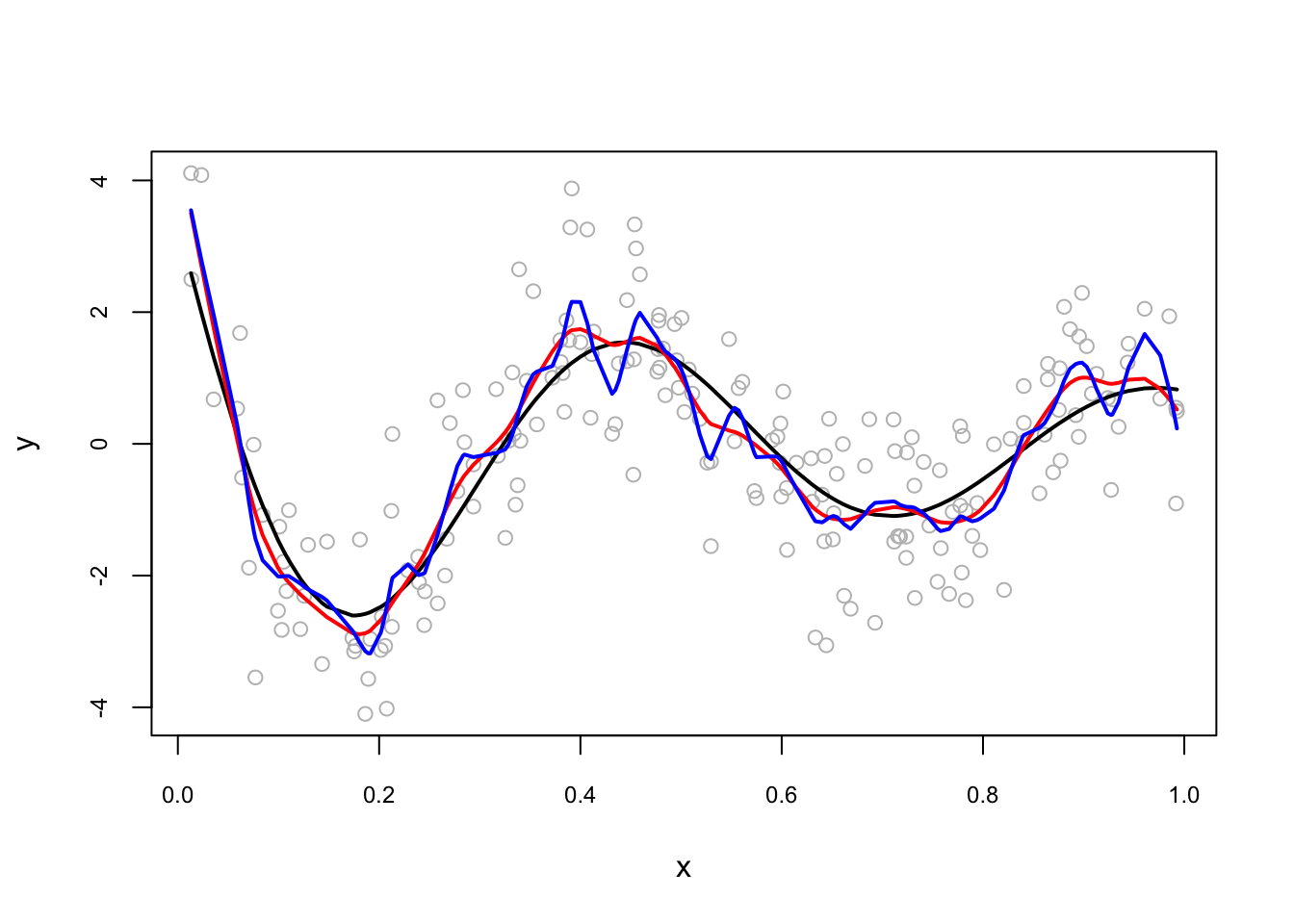

And when we use automated selection of knots:

plot(x, y, col = "gray", cex.main = 0.80, cex.axis = 0.75)
lines(x[order(x)], dgm[order(x)], lwd = 2, col = "black") # DGM
#lines(smooth.spline(x,y, cv = FALSE), lwd = 2, col = "blue") # With GCV
lines(smooth.spline(x,y), lwd = 2, col = "red") # With LOOCV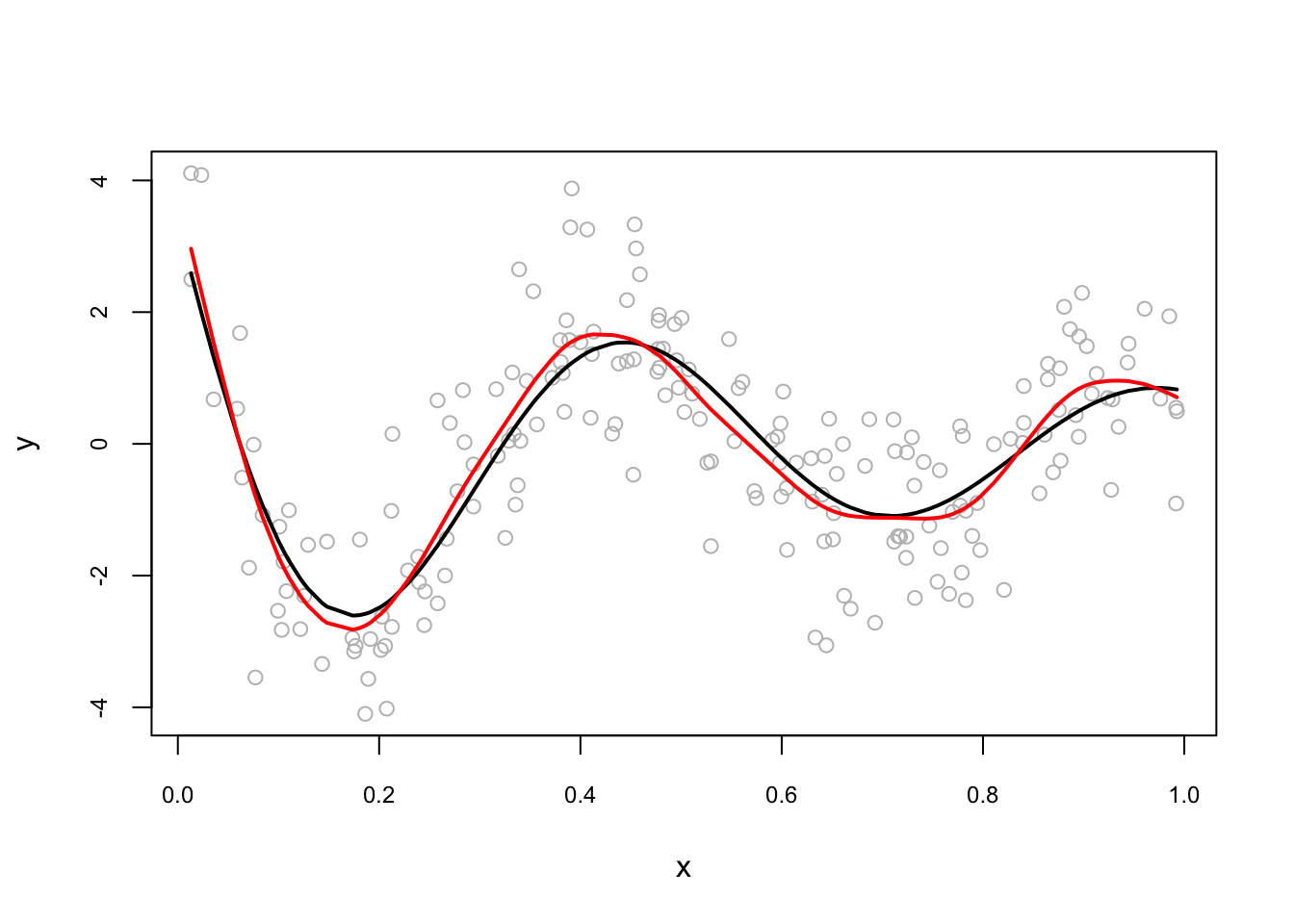

Note that there are other packages for smoothing splines like npreg that uses ss()⁶.

In theory, nonparametric regression estimations can be easily extended to several regressors but in practice, good precision may require a huge number of observations without any graphical tools to make interpretation. However, there are two common methods that have been used in multivariable settings: GAM (generalized additive regression splines) and MARS (multivariate adaptive regression splines).

6.4 MARS - Multivariate Adaptive Regression Splines

Linear models can be adapted to nonlinear patterns in the data by manually adding model terms (i.e. squared terms, interaction effects). However, to do so you must know the specific nature of the nonlinearity a priori. Alternatively, there are numerous algorithms that are inherently nonlinear. When using these models, the exact form of the nonlinearity does not need to be known explicitly or specified prior to model training. Rather, these algorithms will search for, and discover, nonlinearities in the data that help maximize predictive accuracy⁷.

As we have seen before, we can extend linear models to capture non-linear relationships by including polynomial parameters. However, it is generally unusual to use degree greater than 3 or 4, and even if we use higher degrees, with multiple interactions and polynomials, the dimension of the model goes out of control. Although useful, the typical implementation of polynomial regression requires the user to explicitly identify and incorporate which variables should have what specific degree polynomials and interactions. With data sets that can easily contain 50, 100, or more variables today, this would require an enormous time to determine the explicit structure of non-linear nature of the model⁸.

Multivariate adaptive regression splines (MARS) can be a solution to capture the nonlinearity aspect of polynomial regression by assessing cutpoints (knots) like in a piecewise regression model. The procedure first looks for the single point across the range of \(X\) values where two different linear relationships between \(Y\) and \(X\) achieve the smallest error. For example, consider a simple one-variable model of \(Y\) ~ \(X\). The MARS procedure will first look for the single point across the range of \(X\) values where two different linear relationships between \(Y\) and \(X\) achieve the smallest error. The results is known as a hinge function \(h(x−a)\) where a is the cutpoint value. Once the first knot has been found, the search continues for a second knot, which results in three linear models. This procedure can continue until many knots are found, producing a highly non-linear pattern. Once the full set of knots have been created, we can sequentially remove knots that do not contribute significantly to predictive accuracy. This process is known as pruning and can be done by cross-validation, as we will see later in this text, to find the optimal number of knots.

Here is a simple application as our first example with the longley dataset that describes 7 economic variables observed from 1947 to 1962 used to predict the number of people employed yearly.

library(earth)

# load data
data(longley)
summary(longley)

##   GNP.deflator         GNP          Unemployed     Armed.Forces  
##  Min.   : 83.00   Min.   :234.3   Min.   :187.0   Min.   :145.6  
##  1st Qu.: 94.53   1st Qu.:317.9   1st Qu.:234.8   1st Qu.:229.8  
##  Median :100.60   Median :381.4   Median :314.4   Median :271.8  
##  Mean   :101.68   Mean   :387.7   Mean   :319.3   Mean   :260.7  
##  3rd Qu.:111.25   3rd Qu.:454.1   3rd Qu.:384.2   3rd Qu.:306.1  
##  Max.   :116.90   Max.   :554.9   Max.   :480.6   Max.   :359.4  
##    Population         Year         Employed    
##  Min.   :107.6   Min.   :1947   Min.   :60.17  
##  1st Qu.:111.8   1st Qu.:1951   1st Qu.:62.71  
##  Median :116.8   Median :1954   Median :65.50  
##  Mean   :117.4   Mean   :1954   Mean   :65.32  
##  3rd Qu.:122.3   3rd Qu.:1958   3rd Qu.:68.29  
##  Max.   :130.1   Max.   :1962   Max.   :70.55

# fit model
fit1 <- earth(Employed ~ ., longley)
summary(fit1)

## Call: earth(formula=Employed~., data=longley)
## 
##                       coefficients
## (Intercept)            -1682.60259
## Year                       0.89475
## h(293.6-Unemployed)        0.01226
## h(Unemployed-293.6)       -0.01596
## h(Armed.Forces-263.7)     -0.01470
## 
## Selected 5 of 8 terms, and 3 of 6 predictors
## Termination condition: GRSq -Inf at 8 terms
## Importance: Year, Unemployed, Armed.Forces, GNP.deflator-unused, ...
## Number of terms at each degree of interaction: 1 4 (additive model)
## GCV 0.2389853    RSS 0.7318924    GRSq 0.9818348    RSq 0.996044

# summarize the importance of input variables
evimp(fit1)

##              nsubsets   gcv    rss
## Year                4 100.0  100.0
## Unemployed          3  24.1   23.0
## Armed.Forces        2  10.4   10.8

#plot
plot(fit1, which = 1, cex.main = 0.80, cex.axis = 0.75)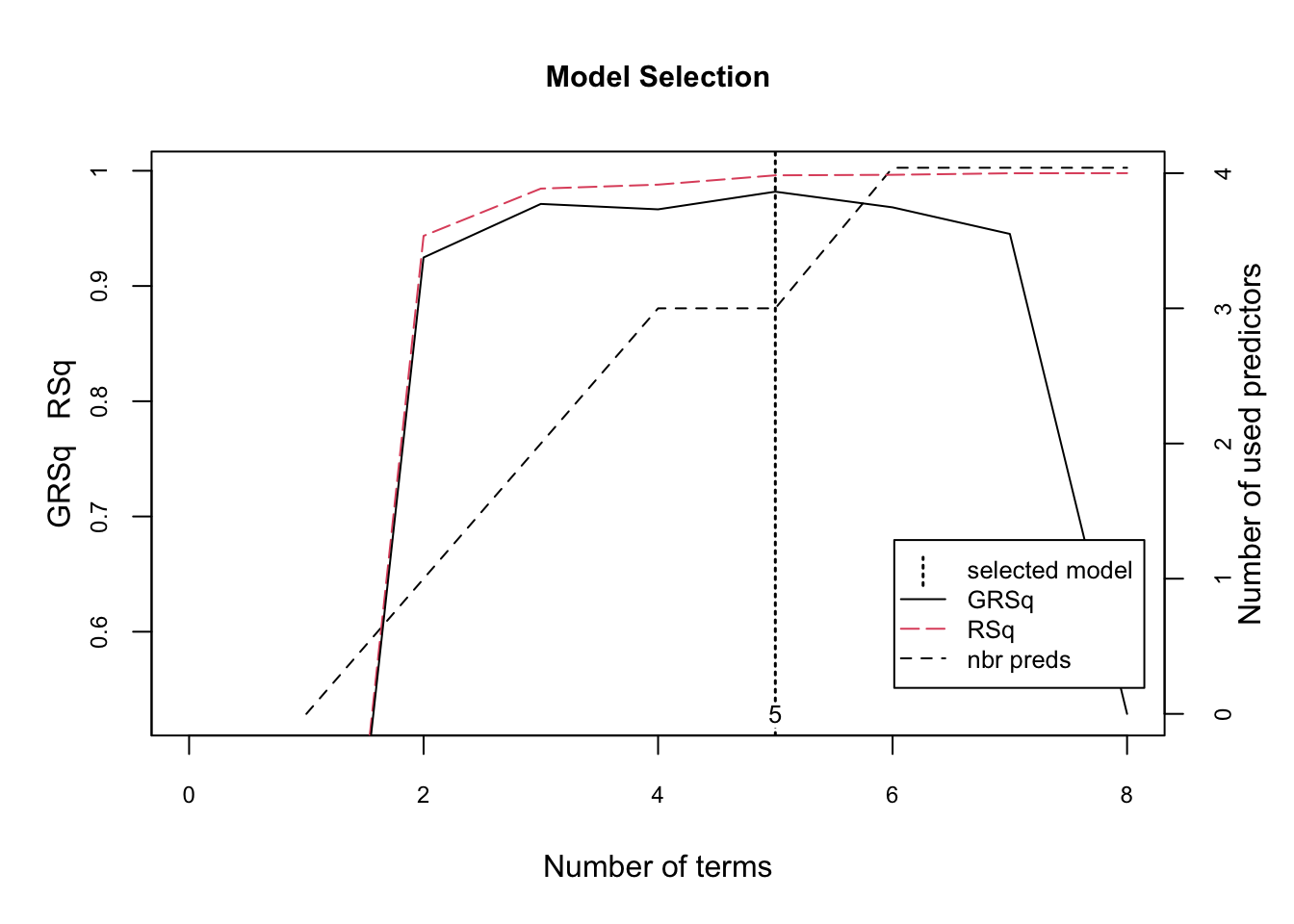

# make predictions
predictions1 <- predict(fit1, longley)

# summarize accuracy for fit1
mse <- mean((longley$Employed - predictions1)^2)
mse

## [1] 0.04574327

#Remember this an in-sample fit. We need to use an out-sample MSE
#We'll see that later in the book

The figure illustrates the model selection plot that graphs the GCV (generalized cross-validation) R2 (left-hand y-axis and solid black line) based on the number of terms retained in the model (x-axis) which are constructed from a certain number of original predictors (right-hand y-axis). The vertical dashed lined at 5 tells us the optimal number of non-intercept terms retained where marginal increases in GCV R2 are less than 0.001.

Let’s use another data, Ames Housing data (Cock 2011), which is available by AmesHousing package.

library(AmesHousing)

# Fit a basic MARS model
amesdata <- make_ames()
ames1 <- earth(Sale_Price ~ .,  data = amesdata)
ames2 <- earth(Sale_Price ~ .,  data = amesdata, degree = 2)

# In addition to pruning the number of knots,
# we can also assess potential interactions between different hinge functions.
# In the 2nd model, "degree = 2" argument allows level-2 interactions. 

summary(ames1)

## Call: earth(formula=Sale_Price~., data=amesdata)
## 
##                                coefficients
## (Intercept)                      279490.795
## NeighborhoodNorthridge_Heights    16810.853
## NeighborhoodCrawford              24189.424
## NeighborhoodNorthridge            27618.337
## NeighborhoodStone_Brook           31410.387
## NeighborhoodGreen_Hills          109592.758
## Condition_2PosN                  -96442.914
## Overall_QualGood                  12990.668
## Overall_QualVery_Good             34907.970
## Overall_QualExcellent             84380.868
## Overall_QualVery_Excellent       125196.226
## Overall_CondFair                 -23679.636
## Overall_CondGood                  11521.886
## Overall_CondVery_Good             14138.461
## Bsmt_ExposureGd                   11893.023
## FunctionalTyp                     17341.390
## h(15431-Lot_Area)                    -1.749
## h(Lot_Area-15431)                     0.301
## h(2003-Year_Built)                 -426.978
## h(Year_Built-2003)                 4212.701
## h(1972-Year_Remod_Add)              253.232
## h(Year_Remod_Add-1972)              486.266
## h(1869-Bsmt_Unf_SF)                  19.399
## h(Bsmt_Unf_SF-1869)                -121.684
## h(Total_Bsmt_SF-1822)               125.954
## h(2452-Total_Bsmt_SF)               -31.670
## h(Total_Bsmt_SF-2452)              -221.022
## h(Second_Flr_SF-1540)               320.816
## h(Gr_Liv_Area-3005)                 237.824
## h(3228-Gr_Liv_Area)                 -50.647
## h(Gr_Liv_Area-3228)                -316.547
## h(Kitchen_AbvGr-1)               -22620.827
## h(1-Fireplaces)                   -5701.130
## h(Fireplaces-1)                    8654.214
## h(2-Garage_Cars)                  -5290.463
## h(Garage_Cars-2)                  11400.346
## h(210-Screen_Porch)                 -55.241
## 
## Selected 37 of 40 terms, and 26 of 308 predictors
## Termination condition: RSq changed by less than 0.001 at 40 terms
## Importance: Gr_Liv_Area, Year_Built, Total_Bsmt_SF, Overall_QualExcellent, ...
## Number of terms at each degree of interaction: 1 36 (additive model)
## GCV 506531262    RSS 1.411104e+12    GRSq 0.9206569    RSq 0.9245098

summary(ames2)

## Call: earth(formula=Sale_Price~., data=amesdata, degree=2)
## 
##                                                   coefficients
## (Intercept)                                         304004.163
## NeighborhoodGreen_Hills                             107542.815
## Overall_QualGood                                     28295.297
## Overall_QualVery_Good                                50500.728
## Overall_QualExcellent                                80054.922
## Overall_QualVery_Excellent                          115273.427
## Bsmt_ExposureGd                                      11761.126
## h(5400-Lot_Area)                                        -4.428
## h(Lot_Area-5400)                                         3.752
## h(2003-Year_Built)                                    -497.006
## h(Year_Built-2003)                                    7976.946
## h(Year_Remod_Add-1974)                                 957.791
## h(2452-Total_Bsmt_SF)                                  -54.823
## h(Total_Bsmt_SF-2452)                                   49.902
## h(3228-Gr_Liv_Area)                                    -44.151
## h(Gr_Liv_Area-3228)                                    197.513
## h(2-Fireplaces)                                      -6761.928
## h(Lot_Area-5400) * Overall_CondFair                     -2.710
## NeighborhoodCrawford * h(2003-Year_Built)              399.860
## Overall_QualAverage * h(2452-Total_Bsmt_SF)              6.310
## Overall_QualAbove_Average * h(2452-Total_Bsmt_SF)       11.542
## Overall_QualVery_Good * h(Bsmt_Full_Bath-1)          49827.988
## Overall_QualVery_Good * h(1-Bsmt_Full_Bath)         -12863.190
## Overall_CondGood * h(3228-Gr_Liv_Area)                   4.782
## Mas_Vnr_TypeStone * h(Gr_Liv_Area-3228)               -512.416
## h(Lot_Area-19645) * h(2452-Total_Bsmt_SF)               -0.001
## h(Lot_Area-5400) * h(Half_Bath-1)                       -3.867
## h(Lot_Area-5400) * h(1-Half_Bath)                       -0.397
## h(Lot_Area-5400) * h(Open_Porch_SF-195)                 -0.011
## h(Lot_Area-5400) * h(195-Open_Porch_SF)                 -0.005
## h(Lot_Area-5400) * h(192-Screen_Porch)                  -0.008
## h(2003-Year_Built) * h(Total_Bsmt_SF-1117)              -0.729
## h(2003-Year_Built) * h(1117-Total_Bsmt_SF)               0.368
## h(Year_Built-2003) * h(2439-Gr_Liv_Area)                -5.516
## h(Year_Remod_Add-1974) * h(Mas_Vnr_Area-14)              1.167
## h(Year_Remod_Add-1974) * h(14-Mas_Vnr_Area)             17.544
## h(Year_Remod_Add-1974) * h(Gr_Liv_Area-1627)             1.067
## h(Year_Remod_Add-1974) * h(932-Garage_Area)             -1.132
## h(Year_Remod_Add-1974) * h(Longitude- -93.6278)     -19755.291
## h(Year_Remod_Add-1974) * h(-93.6278-Longitude)       -7450.926
## h(1191-Bsmt_Unf_SF) * h(3228-Gr_Liv_Area)                0.009
## h(Bsmt_Unf_SF-1191) * h(3228-Gr_Liv_Area)               -0.028
## 
## Selected 42 of 49 terms, and 26 of 308 predictors
## Termination condition: RSq changed by less than 0.001 at 49 terms
## Importance: Gr_Liv_Area, Year_Built, Total_Bsmt_SF, Overall_QualExcellent, ...
## Number of terms at each degree of interaction: 1 16 25
## GCV 415202608    RSS 1.132115e+12    GRSq 0.9349626    RSq 0.9394349

# predictions
predictions1 <- predict(ames1, amesdata)
predictions2 <- predict(ames2, amesdata)

# summarize accuracy for ames1 and ames2
mse <- mean(sqrt((amesdata$Sale_Price - predictions1)^2))
mse

## [1] 15345.66

mse <- mean(sqrt((amesdata$Sale_Price - predictions2)^2))
mse

## [1] 13910.27

Now the second model includes interaction terms between multiple hinge functions. For example, \(h(Year\_Built-2003)*h(Gr\_Liv\_Area-2274)\) is an interaction effect for those houses built prior to 2003 and have less than 2,274 square feet of living space above ground.

There are two tuning parameters with a MARS model: the degree of interactions and nprune - the number of retained terms. These parameters are called hyperparameters and we need to perform a grid search to find their optimal combination that maximizes the prediction accuracy. We will have chapter on this subject and examples later. We will learn to built our own syntax for grid search and learn about how to present our results using variable importance plots, like vip(), later.

Here is our simple grid search with Caret library⁹.

library(caret)
library(ggplot2)
library(vip)

# create a tuning grid
grid <- expand.grid(   #see ?expand.grid
  degree = 1:3, 
  nprune = seq(2, 100, length.out = 10) %>% floor()
  )
head(grid)

##   degree nprune
## 1      1      2
## 2      2      2
## 3      3      2
## 4      1     12
## 5      2     12
## 6      3     12

set.seed(123)
# cross validated model
mars <- train(
  x = subset(amesdata, select = -Sale_Price),
  y = amesdata$Sale_Price,
  method = "earth",
  metric = "RMSE",
  trControl = trainControl(method = "cv", number = 10),
  tuneGrid = grid
)

# best model
mars$bestTune

##   nprune degree
## 5     45      1

# plot results
ggplot(mars)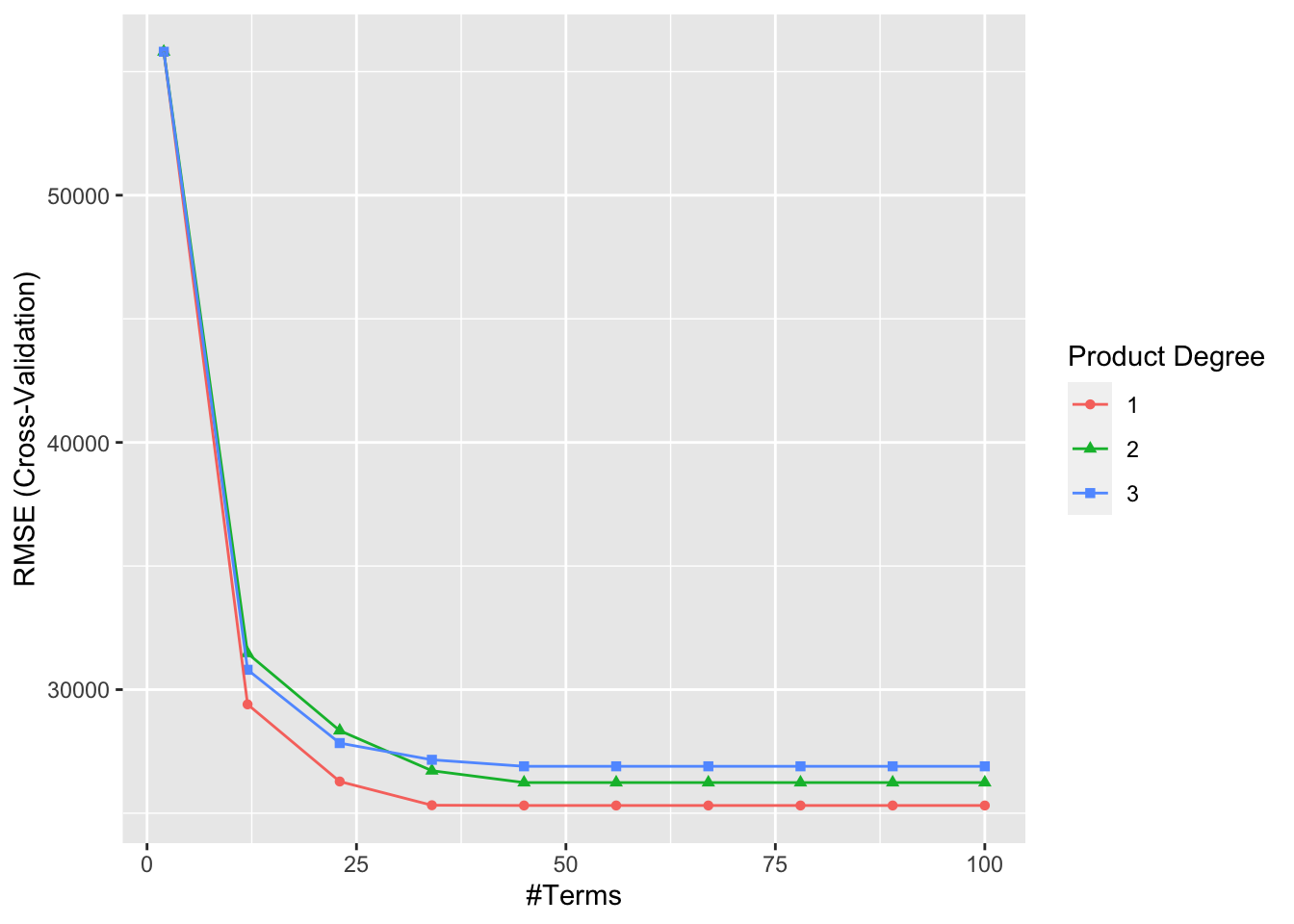

# variable importance plots
vip(mars, num_features = 40, bar = FALSE, value = "gcv") + ggtitle("GCV")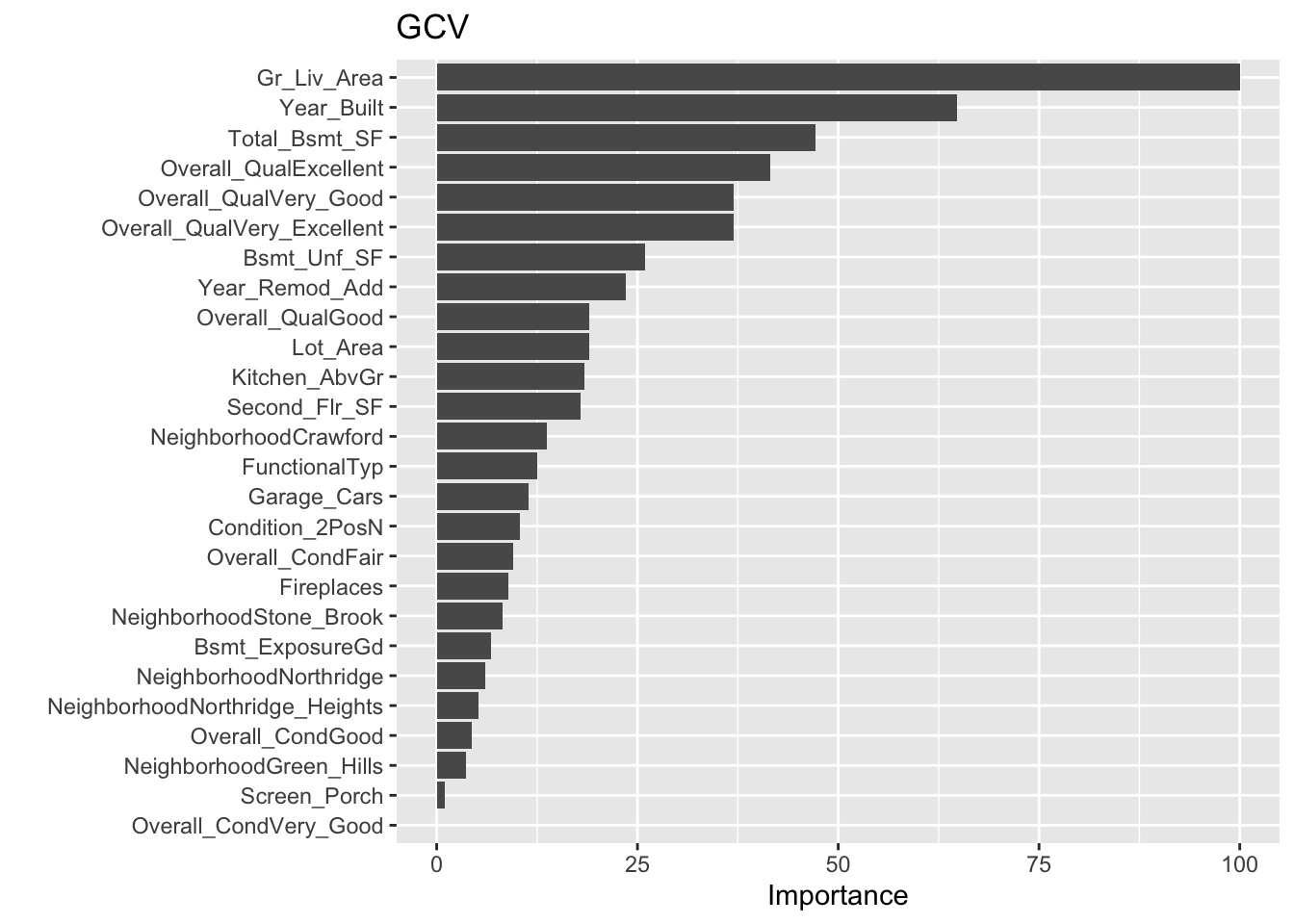

How does this compare to some other linear models for the Ames housing data? That’s the main question that we will ask in related chapters covering other machine learning models.

6.5 GAM - Generalized Additive Model

This is another method for discovering non-linear relationships in a multivariate setting with a nonparametric method. The performance difference between MARS and GAM is well explained by Leathwich, Elith, and Hastie (2006). Here is an excerpt from their paper (Page 189):

Two other commonly used techniques capable of fitting non-linear relationships (…) are neural nets and classification and regression trees. A third alternative, multivariate adaptive regression splines (MARS), has shown promise in recent comparative studies. This technique combines the strengths of regression trees and spline fitting by replacing the step functions normally associated with regression trees with piecewise linear basis functions. This allows the modelling of complex relationships between a response variable and its predictors. In practical terms, MARS has exceptional analytical speed, and its simple rule-based basis functions facilitate the prediction of species distributions using independent data.

And from their abstract:

Results indicate little difference between the performance of GAM and MARS models, even when MARS models included interaction terms between predictor variables. Results from MARS models are much more easily incorporated into other analyses than those from GAM models. The strong performance of a MARS multiresponse model, particularly for species of low prevalence, suggests that it may have distinct advantages for the analysis of large datasets.

GAM uses an iterative estimation process to the following generalized additive model by assuming \(m\) can be decompose as a sum of several functions of dimension one or two (or more):
\[\begin{equation} y=m_{1}\left(x_{1}\right)+m_{2}\left(x_{2}\right)+\cdots+m_{k}\left(x_{k}\right)+\varepsilon \tag{6.16} \end{equation}\]

The estimation to this 2-variable additive model \(y=m_{1}\left(x_{1}\right)+m_{2}\left(x_{2}\right)+\varepsilon\) can be done by the following iterative procedure:

\[ \begin{array}{l}{\text { (1) Select initial estimates } m_{1}^{(0)} \text { and } m_{2}^{(0)}} \\ {\text { (2) Obtain } \hat{m}_{1}^{(i)} \text { by regressing } y-\hat{m}_{2}^{(i-1)} \text { on } x_{1}} \\ {\text { (3) Obtain } \hat{m}_{2}^{(i)} \text { by regressing } y-\hat{m}_{1}^{(i-1)} \text { on } x_{2}} \\ {\text { (4) Repeat steps } 2 \text { an } 3 \text { until no significant changes }}\end{array} \]

Initial estimates can be equal to 0 or obtained by OLS. Extension to more than 2 functions does not lead to the curse of dimensionality problem. Kernel or spline methods can be used for \(m(x)\). Let’s consider the following estimation using a housing data set described below:

\[ \log (\text { price })=X \beta+m_{1}(\text { green })+m_{2}(\text { coord } 1)+m_{3}(\text { coord } 2)+\varepsilon, \]

where price is the housing price - 1135 observations, 1995 in Brest; \(X\) dummies: Studio, T1, T2, T3, T4, T5, house, parking are indicator variables defining the type of building and whether the parking lot exits or not; green is the distance to the closest green park; and coord1, coord2 are geographical coordinates (location). This model is also known as a partially linear model.

data <- read.table("hedonic.dat", header = TRUE)
attach(data) # note that this is not advisable but I use it in this example
library(mgcv)

# Note that a nonlinear transformation of a dummy variable is still a dummy.
# let's add them in X vector
X <- cbind(T1, T2, T3, T4, T5, HOUSE, PARKING)
semip <- gam(LPRIX ~ X + s(GREEN) + s(COORD1) + s(COORD2))

# s() defines smooths in GAM formulae
summary(semip)

## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## LPRIX ~ X + s(GREEN) + s(COORD1) + s(COORD2)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  4.79133    0.04698 101.997  < 2e-16 ***
## XT1          0.06974    0.05737   1.216    0.224    
## XT2          0.38394    0.05173   7.421 2.41e-13 ***
## XT3          0.75105    0.05025  14.946  < 2e-16 ***
## XT4          0.97310    0.05138  18.939  < 2e-16 ***
## XT5          1.13707    0.05666  20.070  < 2e-16 ***
## XHOUSE       0.23965    0.03273   7.321 4.91e-13 ***
## XPARKING     0.22890    0.02400   9.538  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##             edf Ref.df     F p-value    
## s(GREEN)  5.539  6.745 2.552  0.0111 *  
## s(COORD1) 8.289  8.848 7.523  <2e-16 ***
## s(COORD2) 8.323  8.869 7.182  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.672   Deviance explained = 68.1%
## GCV = 0.10301  Scale est. = 0.10011   n = 1070

From these results, we can make standard interpretations: with similar other characteristics: (1) on average, a Studio costs 120.421 francs (\(e^{4.791}\)); (2) a T2 is expected to cost 38.4% more than a Studio; (3) a house is expected to cost 23.9% more than an apartment. We also have results on the nonparametric components. The \(p\)-values correspond to test \(H_0\) : linear vs. \(H_1\) : nonlinear relationship. We can plot the nonparametric components, \(m_1\), \(m_2\) and \(m_3\):

data <- read.table("hedonic.dat", header = TRUE)
attach(data)
semip <- mgcv::gam(LPRIX ~ X + s(GREEN) + s(COORD1) + s(COORD2))
par(mfrow = c(1, 3))
plot(semip, shade = TRUE, shade.col = "pink", ylim = c(-0.5, 0.7))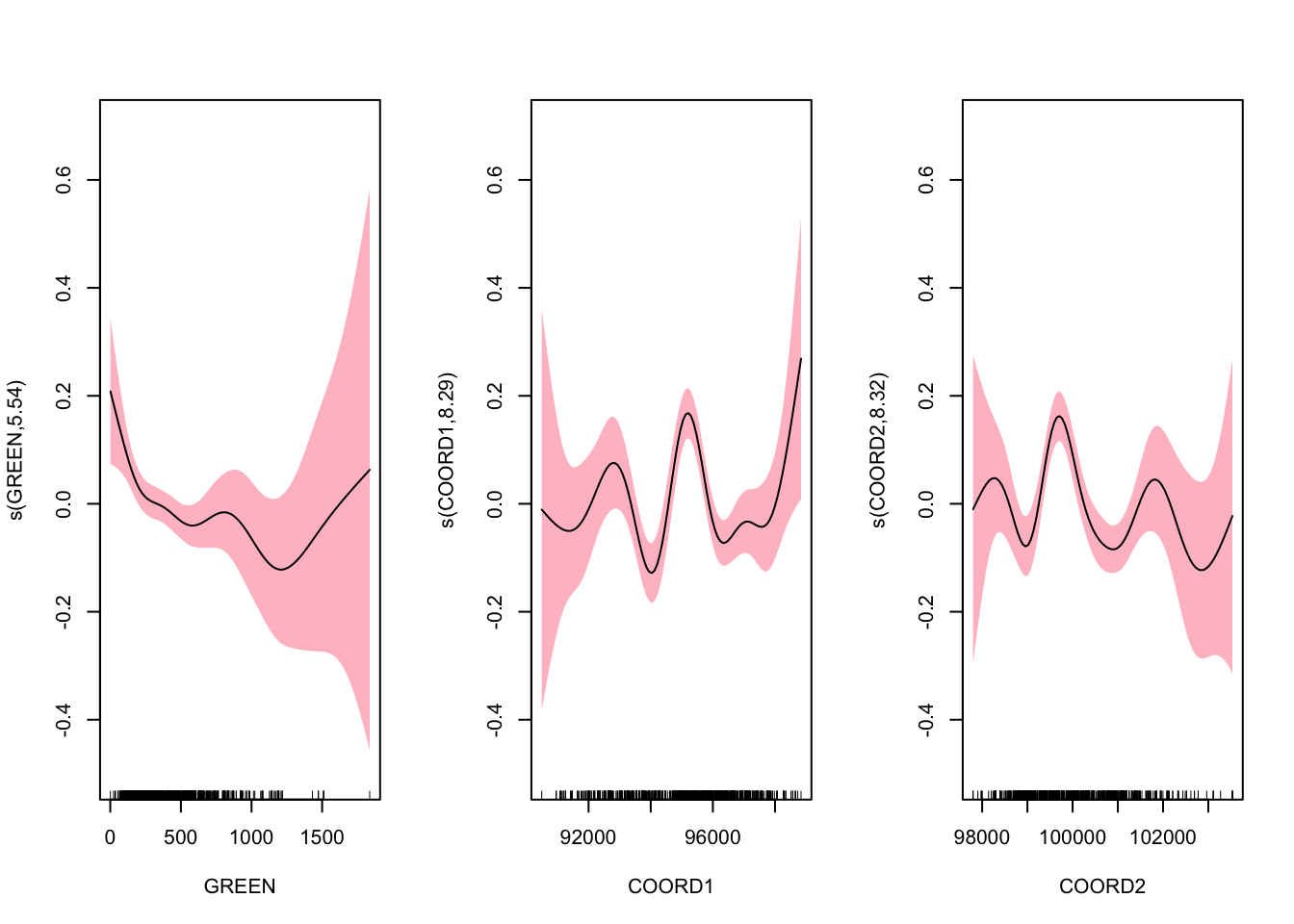

These figures do not suggest simple parametric modeling. The main problem with the model above is that important interactions can be missed. For example, if geographical location is assumed highly nonlinear, we should consider a more flexible model:

\[ \log (\text { price })=X \beta+m_{1}(\text { green })+m_{2}(\text { coord } 1, \text { coord } 2)+\varepsilon \] where spatial dependence is specified fully nonparametrically.

semip2 <- gam(LPRIX ~ X + s(GREEN) + s(COORD1, COORD2))
summary(semip2)

## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## LPRIX ~ X + s(GREEN) + s(COORD1, COORD2)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  4.77597    0.04641 102.916  < 2e-16 ***
## XT1          0.08030    0.05628   1.427    0.154    
## XT2          0.38691    0.05102   7.583 7.50e-14 ***
## XT3          0.76278    0.04959  15.383  < 2e-16 ***
## XT4          0.99325    0.05079  19.555  < 2e-16 ***
## XT5          1.13897    0.05594  20.361  < 2e-16 ***
## XHOUSE       0.23827    0.03247   7.339 4.36e-13 ***
## XPARKING     0.24428    0.02426  10.069  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##                     edf Ref.df     F p-value    
## s(GREEN)          6.487  7.626 2.074  0.0445 *  
## s(COORD1,COORD2) 24.063 27.395 6.714  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.685   Deviance explained = 69.6%
## GCV = 0.099791  Scale est. = 0.096196  n = 1070

vis.gam(semip, view =c("COORD1", "COORD2"), phi = 20)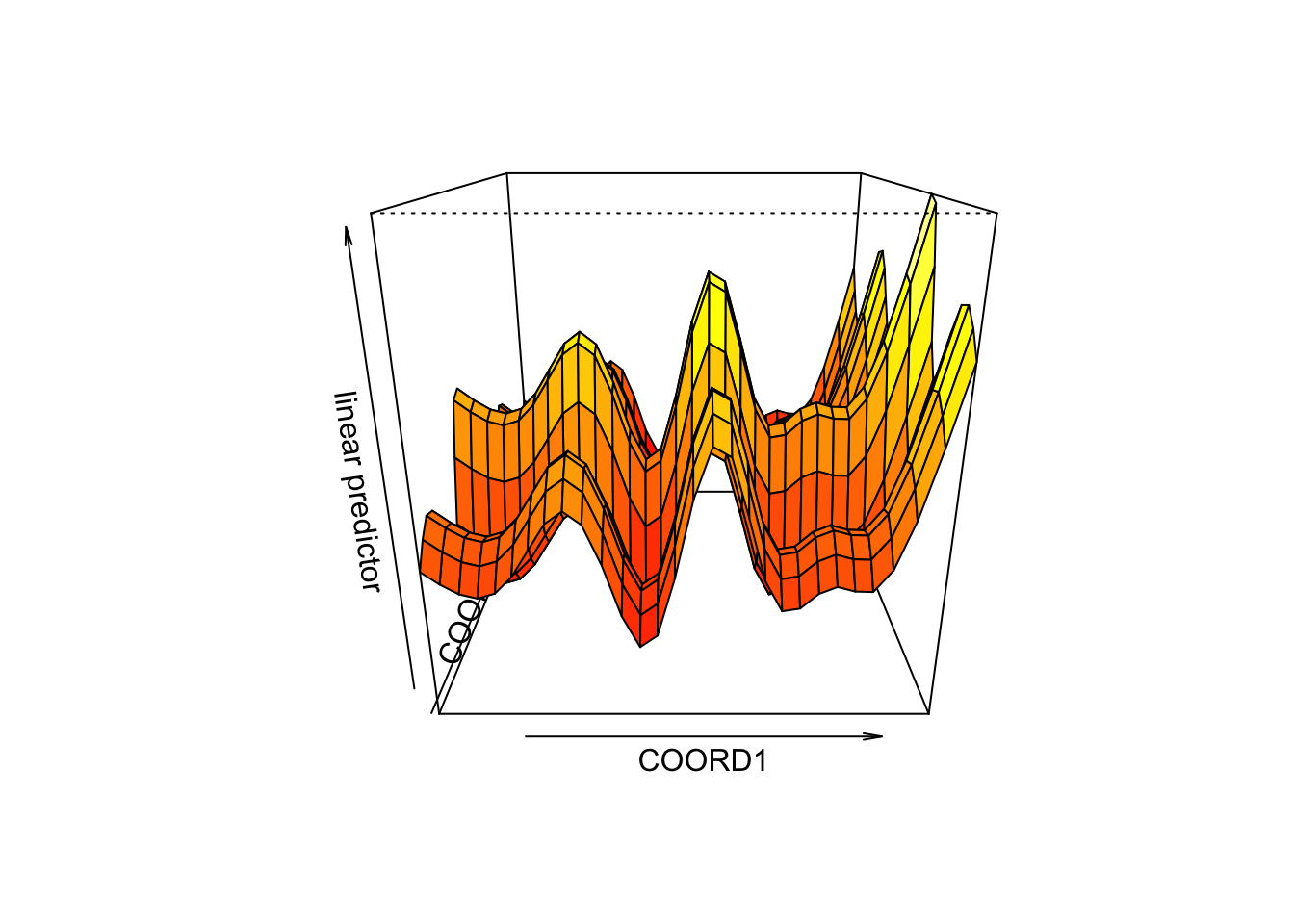

GAMs provide a useful compromise between linear and fully nonparametric models:

semip3 <- gam(LPRIX ~ X + GREEN + COORD1 + COORD2)
summary(semip3)

## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## LPRIX ~ X + GREEN + COORD1 + COORD2
## 
## Parametric coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  7.211e+00  1.096e+00   6.577 7.54e-11 ***
## XT1          6.455e-02  6.042e-02   1.068 0.285597    
## XT2          3.859e-01  5.444e-02   7.089 2.47e-12 ***
## XT3          7.548e-01  5.235e-02  14.418  < 2e-16 ***
## XT4          9.576e-01  5.309e-02  18.037  < 2e-16 ***
## XT5          1.141e+00  5.860e-02  19.462  < 2e-16 ***
## XHOUSE       2.741e-01  3.274e-02   8.371  < 2e-16 ***
## XPARKING     2.417e-01  2.454e-02   9.850  < 2e-16 ***
## GREEN       -4.758e-05  4.470e-05  -1.064 0.287435    
## COORD1       1.909e-05  7.111e-06   2.685 0.007365 ** 
## COORD2      -4.219e-05  1.148e-05  -3.674 0.000251 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## 
## R-sq.(adj) =   0.63   Deviance explained = 63.3%
## GCV = 0.11418  Scale est. = 0.113     n = 1070

As you can see from these examples, GAM becomes an important tool to understand of the model should be estimated as a linear function or a complex non-linear function. We can even see if a specific variable should have a non-linear part. For example, if we want to know coordinates should be included additively, linear , or nonparametrically, we can use GAM and then compare performances of those different models and make a decision.

semip4 <- gam(LPRIX ~ X + GREEN + COORD1 + COORD2)
summary(semip3)

## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## LPRIX ~ X + GREEN + COORD1 + COORD2
## 
## Parametric coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  7.211e+00  1.096e+00   6.577 7.54e-11 ***
## XT1          6.455e-02  6.042e-02   1.068 0.285597    
## XT2          3.859e-01  5.444e-02   7.089 2.47e-12 ***
## XT3          7.548e-01  5.235e-02  14.418  < 2e-16 ***
## XT4          9.576e-01  5.309e-02  18.037  < 2e-16 ***
## XT5          1.141e+00  5.860e-02  19.462  < 2e-16 ***
## XHOUSE       2.741e-01  3.274e-02   8.371  < 2e-16 ***
## XPARKING     2.417e-01  2.454e-02   9.850  < 2e-16 ***
## GREEN       -4.758e-05  4.470e-05  -1.064 0.287435    
## COORD1       1.909e-05  7.111e-06   2.685 0.007365 ** 
## COORD2      -4.219e-05  1.148e-05  -3.674 0.000251 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## 
## R-sq.(adj) =   0.63   Deviance explained = 63.3%
## GCV = 0.11418  Scale est. = 0.113     n = 1070

detach(data)

GAMs are based on a hypothesis of additive separability. They are helpful for reduction of the dimension of the model and they don’t have the curse of dimensionality problem. But, unlike MARS, they miss possible important interactions (we can add them manually, though). Therefore, although a strong nonlinearity between \(x_i\) and \(y\) can be captured, it is identical for all values of other regressors.

References

Ahamada, Ibrahim, and Emmanuel Flachaire. 2011. Non-Parametric Econometrics. Oxford University Press.

Charpentier, Arthur. 2015. “On Some Alternatives to Regression Models.” Freakonometrics. https://freakonometrics.hypotheses.org/19424.

———. 2016. “Regression with Splines: Should We Care about Non-Significant Components?” Freakonometrics. https://freakonometrics.hypotheses.org/47681.

Cock, Dean De. 2011. “Ames, Iowa: Alternative to the Boston Housing Data as an End of Semester Regression Project.” Journal of Statistics Education 19 (3). http://jse.amstat.org/v19n3/decock.pdf.

Fox, John, and Sanford Weisberg. 2018. Nonparametric Regression in r: An Appendix to an r Companion to Applied Regression. 3rd ed. SAGE Publishing. https://socialsciences.mcmaster.ca/jfox/Books/Companion/appendices/Appendix-Nonparametric-Regression.pdf.

———. 2022b. Notes for Predictive Modeling. https://bookdown.org/egarpor/PM-UC3M/.

Leathwick, J. R., J. Elith, and T. Hastie. 2006. “Comparative Performance of Generalized Additive Models and Multivariate Adaptive Regression Splines for Statistical Modelling of Species Distributions.” Ecological Modelling 199 (2): 188–96. https://www.sciencedirect.com/science/article/pii/S0304380006002572.

---

2. For more theoretical explanations, see the link here to one of the good sources) (Fox and Weisberg 2018)↩︎

3. Without theoretical background, which can be found at (Fox and Weisberg 2018) and (García-Portugués 2022b). We will see several important applications later.↩︎

4. if N is the number of data points and span= 0.5, then for a given x, loess will use the 0.5*N closest points to x for the fit. Usually span should be between 0 and 1. When its larger than 1, then the regression will be over-smoothed↩︎

5. see https://www.rdocumentation.org/packages/freeknotsplines/versions/1.0.1/topics/fit.search.numknots for knot location selection↩︎

6. see: http://users.stat.umn.edu/~helwig/notes/smooth-spline-notes.html.↩︎

7. See more on MARS: http://uc-r.github.io/mars.↩︎

8. See the discussion on this here https://freakonometrics.hypotheses.org/19424 (Charpentier 2015).↩︎

9. Caret package provides the most comprehensive machine learning library in R. Although we will not see the details of this library, we will show some examples using Caret.↩︎